Geometria
Ll: Przez punkt wspólny C dwóch przecinających się okręgów poprowadzono sieczną równoległą do
prostej przechodzacej przez środki tych okręgów. Sieczna przecieła okręgi w punktach A i B.
Wykaż, że odciek AB jest dłuższy od wszystkich innych odcinkow siecznych przechodzących przez
punkt C.
26 lut 10:45
Ll: i A, B ≠ C zapomniałem dopisać
26 lut 11:05
Ll: Ktoś mógłby pomóc?
26 lut 12:00
naszybko: innymi slowy wykaz, ze odcinek AB to średnia okręgu przechodzącego min. przez punkt C
26 lut 12:17
naszybko: średnica
26 lut 12:17
Ateusz: @naszybko

xD
26 lut 12:24
Ll: To jest chyba niemożliwe, bo punkty A B C są wspołliniowe.
26 lut 12:25
janek191:
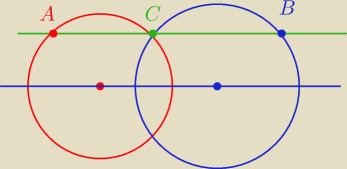
26 lut 14:58
Ll: Dokładnie, zatem jak można to udowodnić?
26 lut 15:23
aa:
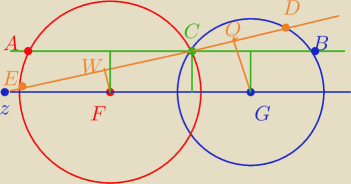
FG=0,5AB
26 lut 15:37
aa: Z zamiast z*
∡EWF=∡EQG=90
o
WQ=0,5ED
WF||QG
| | ZF | |
ZF>ZW (przeciwprostokątna ΔZFW) ⇔ |
| >1 |
| | ZW | |
| | FG | | ZF | |
z talesa |
| = |
| >1 ⇔FG>WQ |
| | WQ | | ZW | |
0,5AB>0,5ED /*2
−−−−− AB>ED −−−−−
26 lut 15:44
 xD
xD

 FG=0,5AB
FG=0,5AB