Funkcje trygonometryczne/uzasadnij Hope: Uzasadnij, że nierówność jest spełniona dla dowolnego kąta α (α jest kątem ostrym) a) sinα*cosα≤1/2 b) tgα+ctgα≥2

Pytający: zacznijmy od tego, że sin(2x)≤1 (zbiór wartości funkcji sinus) 2sinxcosx ≤ 1 (korzystamy ze wzoru na sin(2x) )

	1
sinxcosx≤
	2

b) skoro x jest kątem ostrym, to tgx > 0 oraz ctgx > 0, wówczas z nierówności między średnimi, mamy Am ≥ Gm

tgx + ctgx		1
	≥√tgx•ctgx=√tgx•		=√1=1
2		tgx

tgx + ctgx ≥ 2

Hope: Dziękuję, ale niestety nie rozumiem z tego za wiele : ( jestem w pierwszej klasie lo i niestety nie powiedzieli nam na ten temat za dużo, więc czy można rozwiązać podpunkt a) bez wzoru na sin(2x) oraz b) nie korzystając ze średnich? : /

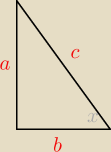
Pytający: Skoro to kąt ostry, to można wyrysować trójkąty prostokątne

	a
sinx =
	c

	b
cosx =
	c

	ab		ab		ab		1
zatem sinxcosx=		=		≤		=
	c2		a2+b2		2ab		2

uzasadnij dlaczego a²+b²≥2ab

ICSP: (a−b)² ≥ 0 co po odpowiednich przekształceniach da

ab
	≤ 2
a2 + b2

Dalej z definicji funkcji trygonometrycznych masz:

	a
sinα =
	c

	b
cosα =
	c

a² + b² = c² zatem

	ab
sinαcosα =		≤ 2
	a2 + b2

Pytający:

	a
tgx =
	b

	b
ctgx=
	a

	a		b		a2+b2		2ab
tgx+ctgx=		+		=		≥		=2
	b		a		ab		ab

Hope: Bardzo dziękuję, już wszystko jasne : )