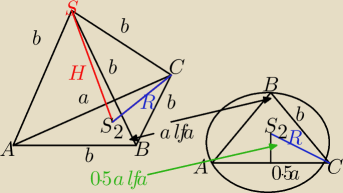
Stereometria fr: W ostrosłupie trójkatnym wszystkie krawedzie boczne i dwie krawedzie podstawy maja długosc b, a kat miedzy równymi bokami podstawy ma miare α. Oblicz objetosc tego ostrosłupa. No i prosiłbym kogoś o sprawdzenie,czy dobrze myślę i licze,bo coś pewnie przedobrzyłem Skoro równe krawędzie boczne to na podstawie można opisać okrąg,podstawa jest trójkątem równoramiennym.

	b2sinα
Czyli Pp=
	2

Z tw. cos. a²=2b²−2b²cosα

a		α
	=sin
2R		2

	a
R=
	α   2sin   2

h=wys.w ΔABC

	4b2−a2
h2=
	4

	h		α
potem		=cos		i wiadomo co dalej
	b		2

Adamm: na trójkącie zawsze da się opisać okrąg

fr: no chodziło mi o spodek wysokości ostrosłupa

Adamm: ja bym pomyślał czy aby na pewno wysokość ostrosłupa przecina podstawę na środku okręgu opisanego na tym trójkącie innymi słowy, uzasadnienie by się tu przydało

Adamm: h jest ci niepotrzebne to H czego szukasz <− tw. Pitagorasa

fr: Tak wiem,tylko chciałem powiązać jakoś te a z b poprzez h,bo wzór na Pp wziąłem używając 'b' a nie 'a' więc jakoś to chciałem powiązać poprzez h właśnie tak czy inaczej dzięki za pomoc

Adamm: tylko że b masz dane a a nie masz dane

iteRacj@:

	α
Kąt zaznaczony kolorem zielonym ma miarę α a nie		.
	2

	1
Jeżeli |AB|=|BC|=b, to |<ABC|=α → |<AS2C|=2α →		|<AS2C|=α
	2