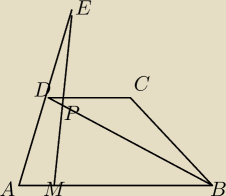
. sylwiaczek: Udowodnij, że IBPI=6IPDI jesli wiadomo ze IAEI=3IADI i IMBI=4IAMI

wredulus_pospolitus: AB || DC

sylwiaczek: tak, to jest trapez

sylwiaczek: pomoze ktos?

oli: Trójkąt AME jest podobny do trójkąta DNE (kąty MAE i NDE są równe oraz kąty AME i DNE są równe, gdyż proste AB i DC są równoległe). Trójkąt MBP jest podobny do trójkąta NDP (kąty MBP i NDP są równe oraz kąty BMP i DNP, gdyż proste AB i DC są równoległe).

oli: N oznacza punkt przecięcia odcinka EM z prostą DC

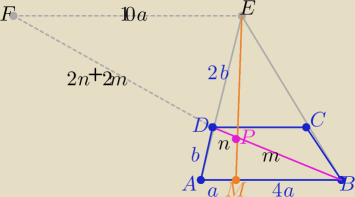
Eta: 1/ rysunek

	2b
2/ trójkąty EFD i ABD podobne w skali k=		=2
	b

to |EF|=10a i |FD|=2|DB|= 2n+2m 3/ trójkąty BMP i EFP podobne

	|FP|		10a		5
to:		=		=
	|P|B|		4a		2

	2n+2m+n		5
		=		⇒ m=6n
	m		2

co daje tezę |BP|=6|PD| ====================== c.n.w

Eta: 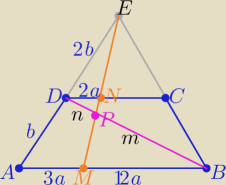2 sposób ( jak podaje oli Z podobieństwa trójkątów AME i DNE |DN|=2a i z podobieństwa trójkątów BMP i DNP

12a		n
	=		⇒ m=6n ⇒
2a		m

|BP|=6|PD| ========== c.n.w. |

sylwiaczek: dziekuje