Ekstrema lokalne funkcji nk: Witam, potrzebuję pomocy ze znalezieniem ekstremów lokalnych funkcji i nie bardzo wiem jak się do tego zabrać: f(x)= 7x/1+x² bardzo proszę o pomoc

Jerzy: Ustal dziedzinę i policz pierwszą pochodną.

nk: wedle moich wyliczeń pochodna to −7x²/(1+x²)² − problem przychodzi jak mam wyznaczyć miejsca zerowe

ICSP: zła pochodna.

	x2 −1
f'(x) = −7
	(x2 + 1)2

Jerzy: Pochodna zła.

	7*(1 + x2) − 7x*2x		7*(1 − x2)
f'(x) =		=
	(1 + x2)2		(1 + x2)2

Teraz miejsca zerowe, czyli: 7*(1 − x²) = 0

nk: Czyli dobrze wnioskuję że maksimum to będzie −1, a minimum 1?

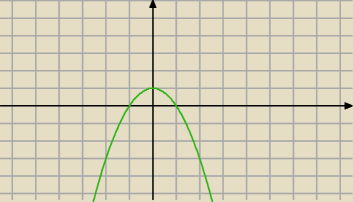
Jerzy: Źle wnioskujesz. Popatrz na wykres: y = 1 − x² i ustal jak zmienia sie znak.

Jerzy: Może niepotrzebnie ICSP wyłączył − 7 przed ułamek w pochodnej i to cie myli.

ICSP:

nk: Czy mogę prosić o jakiś odnośnik do analogicznego przykładu? Powiem szczerze że nie mam pojęcia jak się za to zabrać, przykłady na których działałam to zadania pokroju 𝑦 = x³+x²−x+5 i z tymi nie mam żadnego problemu, ale jak przychodzi do takiego zadania to leżę, nie robiłam takich przykładów nigdy i nie mieliśmy tego w przerabianym materiale, a nie mogę znaleźć jakiegoś podobnego przykładu na internecie żeby móc na czymś bazować.

naszybko: @nk zobacz sobie w tablicach wzor na pochodna ilorazu dwoch funkcji

Jerzy: Aby istniało ekstremum lokalne, to pierwsza pochodna musi sie zerować (warunek konieczny) i zmieniać znak w miejscach zerowych. Tutaj pochodna zeruje sie w punktach x = −1 oraz x = 1. Znak pochodnej zależy tylko od znaku wyrażenia 1 − x² ( patrz rysunek). Dla x ∊ (− ∞,−1) pochodna jest ujemna, a więc funkcja maleje. Dla x ∊ (−1,1) pochodna jest dodatnia, a więc funkcja rośnie. W punkcjie x = −1 funkcja zmieniła sie z malejacej na rosnąca, a więc ma tam minimum. Przeanalizuj sama punkt x = 1

6latek: nk A Krysicki Wlodarski nic nie podaje ?

nk: czyli w punkcie x=1 funkcja ma maksimum lokalne?