Trapez równoramienny-geometria analityczna. Kę: Punkty A(0,−5) oraz D(−3,−1) są kolejnymi wierzchołkami trapezu równoramiennego ABCD, którego osią symetrii jest prosta o równaniu x+2y=0. Oblicz współrzędne pozostałych wierzchołków oraz długość odcinka łączącego środki ramion tego trapezu.

Eta:

	1
k: x+2y=0 ⇒ y=−		x
	2

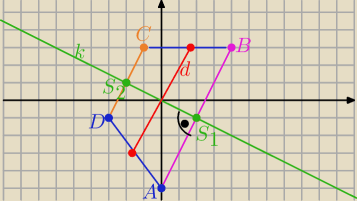
k⊥AB i k⊥DC to a_AB=2 i a_DC=2 AB: y= 2(x−x_A)+y_A ⇒ AB : y=2x−5 i DC: y=2(x−x_D)+y_D ⇒ DC: y=2x+5 Rozwiąż układy równań AB∩k={S₁} i DC∩k={S₂} ........... S₁(2,−1) i S₂=(−2,1) to x_C= 2x_S2−x_D =.... i y_C= 2y_S2−y_D=... ⇒ C(−1,3) oraz x_B=2x_S1−x_A=.. i y_B=2y_S1−y_A=... ⇒B(4,3)

	|AB|+|DC|
d=		= .............
	2

Kę: Dziękuję bardzo

Eta: Na zdrowie