trójkąt asdf: Na boku AC trójkąta ABC obrano punkt D tak że |AD|: |AC|=1:3 a na boku BC obrano punkt E tak że |BE|: |EC|=3:1 Odcinki AE i BD przecinają się w punkcie M. Prosta CM przecina bok AB w punkcie F i wiedząc że pole trójkąta DMC=14 W jakim stosunku punkt M dzieli odcinek CF ?

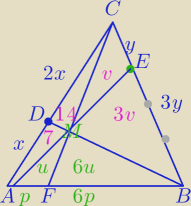
Mila: Twierdzenie Cevy. https://pl.wikipedia.org/wiki/Twierdzenie_Cevy P− pole ΔABC 1) z tw. Cevy

AF		3y		2x
	*		*		=1
FB		y		x

AF		1
	=
FB		6

==========

	2
2) PΔCDB=		P
	3

	1
PΔAEC=		P
	4

	2
⇔14+4v=		P
	3

	1
21+v=		P
	4

	63
v=		, P=210
	2

4v=126 3)

	1
P{ΔDAP=		P
	3

1
	*210=7+7u
3

70=7+7u u=9 6u=54 4)

CM
	=U{P{ΔCMB}}{PΔMFB − Δ maja tę samą wysokość opuszczoną CF z p. B
MF

CM		126		7
	=		=
MF		54		3

================ posprawdzaj rachunki.

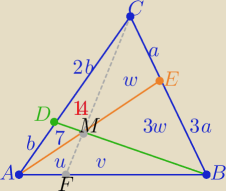Eta: bez Cevy

	1
P(AMD)=		*14= 7
	2

w ΔAEC i AEB : 3(7+14+w)=u+v+3w ⇒ u+v=63 w ΔABD i BDC : 2(7+u+v)=4w+14 ⇒ 4w=126

	u		7+14
w ΔAFC i FBC :		=		⇒ v= 6u to u+6u=63 ⇒ u=9
	v		4w

	|CM|		7+14		7
zatem w ΔAFC :		=		=
	|MF|		9		3

|CM| : |MF|= 7:3 ===============