Trzy różne półproste ile mają wspólnych punktów jezowj: Witam. Mam kłopot z ustaleniem ilości wspólnych punktów dla trzech różnych półprostych. Wiem, że podobny problem był już poruszany ale dla dwóch półprostych. Proszę o podpowiedź.

jezowj: Zapytałem, bo nie jestem do końca pewny. Rozważałem wariant prostych leżących równolegle do siebie. Na każdej z nich są dwie półproste. Który punkt jest punktem wspólnym dla trzeciej półprostej? Dlatego proszę o odpowiedź.

a:

n 2
	?

ABC: "Rozważałem wariant prostych leżących równolegle do siebie. Na każdej z nich są dwie półproste." ile jest tych prostych równoległych do siebie?

jezowj: Rozważałem dwie proste równoległe, bo wtedy półproste leżą na dwóch różnych prostych. Wtedy trzecia półprosta nie ma punktu wspólnego. Pytanie dotyczy ilości wspólnych punktów dla trzech różnych półprostych. Nie jest określone ich położenie.

jezowj: ... ani ilość prostych.

ABC: no to może być nieskończenie wiele punktów wspólnych

6latek:

jezowj: Wydaje mi się, że na prostej mogą być dwie półproste. Może dlatego, że półprosta dzieli prostą na połowę. Poza tym w zadaniu mam cztery warianty odpowiedzi: 0 (zero); 1; 2; 3. Wynika z tego, że każda odpowiedź może być prawidłową.

jezowj: @6latek. Też myślałem o takim rozwiązaniu.

jezowj: ABC: niebieską część na prostej nazwałbym odcinkiem, bo jest z ograniczona z obu stron.

ABC: to są trzy półproste o tym samym zwrocie, zielona półprosta jest częścią wspólną

jezowj: Rozumiem, przepraszam.

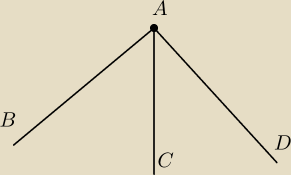
jezowj: ABC. Raczej skłaniałbym się do tego, że punktem wspólnym dla tych trzech prostych jest punkt czerwony (tzn. ten, z którego wychodzi jedna półprosta).

jezowj: Dziękuję bardzo wszystkim za wyjaśnienia, (p)odpowiedzi i pomoc.