pole trójkąta matma3: 1// W trójkącie ABC dwa boki mają długość 4 i 6 a odcinek dwusiecznej kąta między nimi zawartego w tym trójkącie ma długość 4 Oblicz pole tego trójkąta 2// W trójkącie ABC o bokach długości 4 i 6 poprowadzono środkową na trzeci bok, której długość jest równa 3 Oblicz pole tego trójkąta

asia: masz odpowiedzi? czy w pierwszym wychodzi 10√11/3 ?

matma3: Niestety ale nie mam odpowiedzi

Mila:

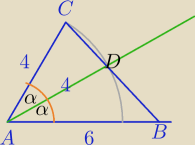
	1
PΔABC=		*6*4*sin2α=12sin2α
	2

	1		1
12sin2α=		*4*4 *sinα+		*6*4*sinα
	2		2

12*2 sinα*cosα=8sinα+12sinα⇔

	20		5
24cosα=20 ⇔ cosα=		=
	24		6

	25		11		√11
sin2α=1−		=		⇔sinα=
	36		36		6

2*sinα*cosα=sin(2α)

	√11		5		10√11
sin2α=2*		*		=
	6		6		36

	1		10√11
PΔABC=		*6*4*
	2		36

	10√11
PΔABC=
	3

=================== II sposób z tw. o dwusiecznej kąta i tw. Pitagorasa

Eta:

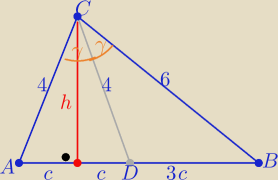
	|AD|		2
1/ z tw. o dwusiecznej		=
	|DB|		3

	4		44
h2=16−c2 i h2= 36−16c2 ⇒ c2=		to h2=
	3		3

	1		100*11
P2=		25c2*h2=
	4		9

	10√11
P(ABC)=
	3

==============

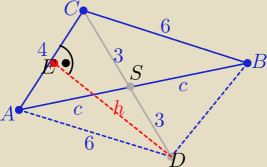
Eta: 1) Budujemy równoległobok ABCD , |CD|=6 ( dwie długości środkowej trójkąta ABC 2)ΔADC jest równoramienny to h=√6²−2²= 4√2

	1		1
P(ABC)=		P(ABCD)=		*4*4√2= 8√2
	2		2