Rozwiąż Równanie Hiera:

|x2−x|+1
	= 1
|x + 1|−x2

Jak rozwiązać te równanie?

zys: zacznij od dziedziny

a47: najlepiej szybko

Hiera: No tak, ale co zrobić potem?

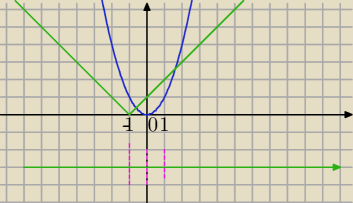
Mila: |x+1|−x²≠0 |x+1|≠x² patrz rysunek ( nad osią OX) x²≠x+1 x²−x−1≠0, Δ=5

	1−√5		1+√5
x≠		i x≠
	2		2

|x²−x|+1=|x+1|−x² 1) x²−x≥0 ⇔x*(x−1)≥0⇔x≤0 lub x≥1 x²−x<0 dla x 2) x+1≥0⇔x≥−1 Teraz przedziałami: a) x<−1 x²−x+1=−x−1−x² 2x²=−2 brak rozwiązań b)x ∊<−1,0> x²−x+1=x+1−x² 2x²−2x=0 x=0 lub x=1 ∉D c) x∊(0,1) −x²+x+1=x+1−x² 0=0 , każda liczba x∊<0,1) spełnia równanie d) x≥1 x²−x+1=x+1−x² 2x²−2x=0 x=0∉D lub x=1 Odp. x∊<0,1>