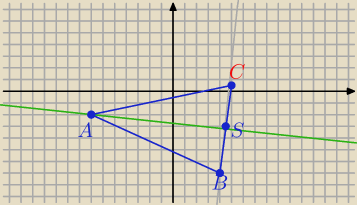
geo anal a47: Punkty A = (− 7,− 2) i B = (4,− 7) są wierzchołkami podstawy trójkąta równoramiennego ABC , a wysokość opuszczona z wierzchołka A tego trójkąta zawiera się w prostej o równaniu 2x + 19y + 52 = 0 . Oblicz współrzędne wierzchołka C . Chciałem policzyc to, że punkt C to punkt przecięcia się prostych BC i prostej prostopadłej do prostej AB, na której leży C. Prosta BC to y=19/2x−45, a symetralna do AB wyszła mi y=11/9x−2/3. Punkt przecicecia sie tych prostych to dziwna liczba, a ma wyjsc 6.Wiem, że ten sposob jest elegancki ale pewnie wyszła mi zła symetralna.Mógłby ktos podac bląd w obliczeniach? Srodek AB to (−3/2,−5/2) i prosta AB to y=−9/11x−41/11

Jerzy: Prosta BC to y = 19/2x + 45. Na podstawie czego taki wniosek ?

ABC: prosta BC to prostopadła do wysokości przechodząca przez punkt B prostopadła do 2x+19y+52=0 ma równanie 19x−2y+k=0 19*4−2*(−7)+k=0 k=−90 19x−2y−90=0

	19
y=		x−45
	2

	(−2)+(−7)		9
tutaj jest ok , ale środek AB , druga współrzędna		=−
	2		2

janek191: 2 x + 19 y + 52 = 0

	2		52
y = −		x −
	19		19

Prosta prostopadła

	19
y =		+ b B = ( 4, −7)
	2

więc − 7 = 38 + b ⇒ b = − 45

	19
y =		x − 45
	2

	2		52		19
−		x −		=		x − 45 / * 38
	19		19		2

− 4 x − 104 = 361 x − 1710 365 x = 1606 x = 4,4 y = − 3,2 S = ( 4,4 ; −3,2 ) → BS = [ 0,4, 3,8 ] C = ( 4,4 +0,4; −3,2 +3,8) = ( 4,8 ; 0,6 ) ===============================

ABC: janek podstawą trójkąta równoramiennego jest AB, ta wysokość na twoim rysunku nie musi spadać na środek

janek191: Pomyłka − źle przeczytałem

a47: Ok, już widzę błąd, liczyłem dla A(−7,2) a nie −2. No cóż