. sylwiaczek: wysokosci rownolegloboku wynosza 2,4 i 4 a jego obwod jest rowny 16. oblicz dlugosci bokow rownolegloboku oblicz cosinus kata rozwartego miedzy przekatnymi tego rownolegloboku dlugosci bokow obliczylam: 5, 3 a jak obliczyc cosinus?

zys: ... znasz boki i wysokości ... znasz więc i pole Policz przekątne ... wykorzystaj wzór na pole czworąta w zależności od przekątnych ... policzysz sinus kąta ... i policzysz jego cosinus

pabel: oblicz pole, a potem ze wzoru P=1/2ab*sinx oblicz sinusa kąta ostrego majac sinusa mozesz obliczyc cosinusa kąta ostrego między scianami ab mając cosinusa mozesz zastosowac twierdzenie cosinusow i obliczyc jedna z przekatnych wiesz ile wynosi sinus kąta ostrego między a i b wiec wiesz ile stopni wynosi ten kąt kąt rozwarty między a i b wynosi (180−x) −−> stąd obliczasz cosinus tego kąta i teraz znów mozesz zastosowac tw. cosinusa, ale tym razem na drugą przekątną. i teraz masz obliczone dwie przekątne. jest taki wzor P=1/2*e*f*siny (y to kąt ostry między przekątnymi) wiesz ile wynosi pole, wiesz ile wynosi e oraz f, więc możesz obliczyć tego sinusa jak juz masz sinusa kąta ostrego między przekątnymi, to wiesz ile stopni ma ten kąt cosinus kąta którego szukasz wynosi 180−y no i rozwiązane, szukasz tylko cosinusa kąta który ci wyszedł

pabel: P=ab*sinx powinno byc

pabel: kąt cosinusa którego szukasz wynosi 180−y*

Jerzy: @ zys..... możesz podać ten wzór na pole czworokąta w zależności od przekątnych ?

Jerzy: @pabel .... 12 = 3*5*sinx ⇔ sinx = 3/4. Ile wynosi x ?

Jerzy: sinx = 4/5 oczywiście.

pabel: @Jerzy nie jest jej to potrzebne do obliczenia cosinusa mozna przeciez z jedynki obliczyc cosinusa a jesli wyjdzie brzydki sinus kąta ostrego między przekątnymi, no to można po prostu z twierdzenia cosinusow bedzie miala polowe jednej przekatnej i polowe drugiej przekatnej to moze obliczyc a²=(1/2e)²+(1/2f)²−2*1/2e*1/2f*cos alfa ma przeciez dane wszystkie oprocz cos alfa, ktory chce policzyc

pabel: a jesli wyjdzie jej brzydki sinus kąta ostrego miedzy a i b to cosinus kąta rozwartego to będzie 180−x (x−kąt ostry między a i b) czyli −cosx które moze policzyc z jedynki tryg znając obliczony juz sinx

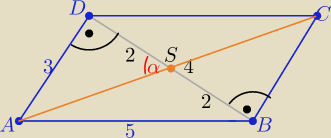
Eta: Z danych w zadaniu wynika ,że a=5 b=3 to równoległobok składa się z dwóch trójkątów prostokątnych zatem w ΔASD |AS|=√3²+2²=√13

	2		2√13
cosα=		=
	√13		13

=================== i po "ptokach "

Jerzy: @panel....możesz pokazać to Twoje rozwiązanie.

Eta: Terza dopiero doczytałam,że ma być cosinus kąta rozwartego

	2√13
zatem cos (180o−α)= −cosα= −
	13

==========

Eta: I co? sylwiaczek ... "kumasz" ? czy dalej milczysz i za chwilę będziesz wrzucać następną porcję zadanek!

Jerzy: Trawi podpowiedź @pabel

Eta:

6latek: Dzien dobry Eta Przepraszam ze sie wczoraj nie przywitalem . A Ty Jerzy nie czepiaj się dziecka

Eta: @pabel od kiedy to, równoległobok ma "ściany" ?

pabel: P=3*4=12 5*3*sinx=12

	4
sinx=
	5

	16
cos2x=1−
	25

	3
cosx=
	5

z tw. cosinusów :

	3
|DB|2=9+25−30*
	5

|DB|²=16 |DB|=4

	1
|SB|=		|DB|=2
	2

	3
cosy=cos(180−x)=−cosx=−		(y−kąt rozwarty między a i b)
	5

	3
|AC|2=25+9−30*−
	5

|AC|²=13 |AC|=2√13

	1
|SA|=		|AC|=√13
	2

|AB|²=|SA|²+|SB|²−2|SA|*|SB|*cosb 25=13+4−4√13cosb

	−8		−2√13
cosb=		=
	4√13		13

@6latek Z jakiego powodu nazywasz mnie dzieckiem? Mam 18 lat @Jerzy @6latek Niepotrzebne złośliwości...

6latek: Nie powiem Ci

Eta: @pabel ............................. ale się opisałeś Na maturze zabraknie Ci czasu na pozostałe zadania !

pabel: @Eta Pisałem to 5−10minut. Nie w każdym zadaniu podane są boki o długościach odpowiednim trójkom pitagorejskim. @6latek Trudno, naprawdę, jakoś to przeżyję.

ABC: matur w tym roku nie będzie bo strajk nauczycieli

6latek: ABC Nie cieszylbym sie tak . Juz tak bylo i zonk

Maciess: Oba sposoby są dobre. Sposób Ety jak zwykle sprytny i szybki. Pokazuje, że trzeba szukać najkrótszej drogi, ale tak jak mowi pabel nie zawsze autor zadania ułatwia nam sprawe albo czegoś nie zobaczymy więc trzeba umieć dać sobie rade inną metodą.

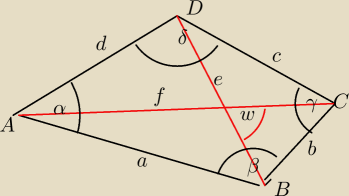
6latek: W dowolnym czworokacie wypuklym w− kąt ostry miedzy przekatnymi P= 0,5*e*f*sin (w) f²*f²= a²*c²+b²*d²−2*a*b*c*d−cos(2x) gdzie (2x)= α+γ lub β+δ

6latek: e²*f²=

6latek: Poprawie jeszcze raz e²*f²= a²*c²+b²*d²−2*a*b*c*d * cos(2x) itd Przepraszam