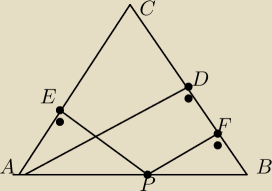
 Na podstawie trojakta rownoramiennego ABC obrano dowolny punkt P
Wykaz ze suma odleglosci punktu P od ramion AC i BC rowna sie sumie dlugosci wysokosci trojkata
poprowadzonej z wierzcholka A
Rysunek do zadania powinien byc dobry
Na podstawie trojakta rownoramiennego ABC obrano dowolny punkt P
Wykaz ze suma odleglosci punktu P od ramion AC i BC rowna sie sumie dlugosci wysokosci trojkata
poprowadzonej z wierzcholka A
Rysunek do zadania powinien byc dobry
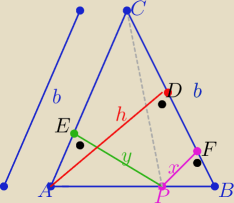 |PF|=x , |PE|=y , |AD|=h
|PF|=x , |PE|=y , |AD|=h
| x*b | y*b | h*b | ||||
P(ABC)= | + | i P= | ⇒ x+y=h | |||
| 2 | 2 | 2 |