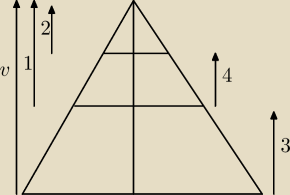
 Stożek o objętości V przecięto dwoma płaszczyznami równoległymi do podstawy od wierzchołka
wysokość podzielona w stosunku 1:2:3. Znaleźć objętość powstałej w ten sposób części środkowej
stożka.
Pytanie do rozwiązania(korzystałem z podobieństwa trójkątów):
k1−v=1/2 => v1= 1/8V
V2=1/64V
V3=V−1/8=7/8V
V4=V−7/8V−1/64V=7/64V
Jednak w odpowiedziach jest 13/108V.
Stożek o objętości V przecięto dwoma płaszczyznami równoległymi do podstawy od wierzchołka
wysokość podzielona w stosunku 1:2:3. Znaleźć objętość powstałej w ten sposób części środkowej
stożka.
Pytanie do rozwiązania(korzystałem z podobieństwa trójkątów):
k1−v=1/2 => v1= 1/8V
V2=1/64V
V3=V−1/8=7/8V
V4=V−7/8V−1/64V=7/64V
Jednak w odpowiedziach jest 13/108V.
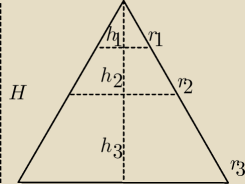 h2=2h1, h3=3h1, H=h1+h2+h3=6h1
r2=3r1, r3=6r1
h2=2h1, h3=3h1, H=h1+h2+h3=6h1
r2=3r1, r3=6r1
| 1 | 1 | |||
V=V1+2+3= | H*π(r3)2= | 6h1*π(6r1)2=72π*h1*(r1)2 | ||
| 3 | 3 |
| 1 | π | 1 | ||||
V1= | h1*π(r1)2= | h1*(r1)2 → V1= | V | |||
| 3 | 3 | 216 |
| 1 | 1 | |||
V1+2= | 3h1*π(3r1)2=9πh1*(r1)2 → V1+2= | V | ||
| 3 | 8 |
| 1 | 1 | 13 | ||||
V2=V1+2−V1= | V− | V= | V | |||
| 8 | 216 | 103 |
| 13 | ||
*= | V | |
| 108 |