Kąt nachylenia ściany bocznej do płaszczyzny podstawy
Kulfon: Wysokość ostrosłupa prawidłowego czworokątnego jest 4 razy dłuższa od krawędzi jego podstawy.
Ściana boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem α takim, że:
A. cosα=2√65 65
B. sinα=2√65 65
C. cosα=√65 65
C. sinα=√65 65
21 lut 16:42
wredulus_pospolitus:
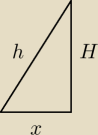
Wystarczy wyznaczyć 'x' który będzie uzależniony od 'a' (krawędź podstawy) i będzie wynosić

Rysunek będzie pomocny
21 lut 16:44
wredulus_pospolitus:
H −−− wysokość ostrosłupa
h −−− wysokość ściany bocznej (którą wyznaczysz z tw. Pitagorasa gdy już policzysz 'x' )
21 lut 16:44
Kulfon: krawędź podstawy − a
H − 4a
x = a/2
(4a)2+(a/2)2 = h2
16a2+ a2/4 = h2
65a2/4 = h2
h = √65a/2
Tak ma to wyglądać?
21 lut 16:49
janek191:
Ułamki piszemy U { } { } bez spacji
21 lut 16:52
wredulus_pospolitus:
noooo
21 lut 16:54
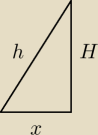 Wystarczy wyznaczyć 'x' który będzie uzależniony od 'a' (krawędź podstawy) i będzie wynosić
Wystarczy wyznaczyć 'x' który będzie uzależniony od 'a' (krawędź podstawy) i będzie wynosić  Rysunek będzie pomocny
Rysunek będzie pomocny