Monotoniczność OVDC: Miałem na egzaminie takie polecenie udowodnij że funkcji lnx⁴ jest monotoniczna (−inf,0), ale jeśli chodziło o przedział x to przecież D:(o,inf), a jeśli chodziło o przedział wartości to czy zasugerowanie wykresu, oraz podstawy logarytmu jest wystarczające i czy o to właśnie chodziło? Wiem że dobrze by było jakbym też policzył monotoniczność, o ile właśnie o to chodziło.

ABC: "Miałem na egzaminie takie polecenie udowodnij że funkcji lnx⁴ jest monotoniczna" "Wiem że dobrze by było jakbym też policzył monotoniczność, o ile właśnie o to chodziło." nie wiem co bierzesz ale za silne dla ciebie to jest, wróć do jaboli

wredulus_pospolitus: 'zasugerowanie wykresu' −−− a jak chcesz udowodnić, że 'zasugerowany' przez Ciebie wykres jest poprawny? D_f = (0, +∞) ... a niby dlaczego "policzył monotoniczność" −−− znaczy się, że co ?

Jerzy: f'(x) = 4lnx

	1
f'(x) =
	4

f'(x) < 0 ⇔ x ∊ (−∞ ;0) U (0;+∞)

Jerzy:

	1
f'(x) =		oczywiście.
	x

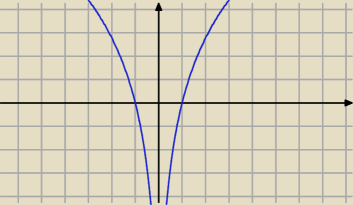
ABC: Jerzy dla x<0 ln(x⁴)=4ln (−x)

wredulus_pospolitus: Jerzy ... a nie szybciej jest: x₁ < x₂ −> |x₁| > |x₂|

	x1
ln(x14) − ln(x24) = ln(		)4 > ln 1 = 0
	x2

Jerzy: @ABC ... oczywiście, pominąłem moduł . @wredulus ....bardzo zgrabnie i z definicji

Jerzy: Pochodną też nieco "uprościlem" , ale bez wpływu na monotoniczność.