kąty w ostrosłupie
pabel: kąty proste w ostrosłupie czworokątnym prawidłowym
Czy ostrosłup czoworokątny, którego podstawą jest kwadrat, charakteryzuje się tym, że jego
krawędzie boczne tworzą z jednym z boków kwadratu kąt prosty?
20 lut 22:06
Mila:
Jeżeli jest prawidłowy czworokątny to nie.
20 lut 22:20
20 lut 22:24
pabel: wklejam zdj. bo nie wiem jak tu rysować.
20 lut 22:26
Mila:
Tak, jak na rysunku może być, ale to nie jest ostrosłup prawidłowy.
Co tam Ci się nie zgadza?
20 lut 23:53
Mila:
Napisz. Jutro pomogę, teraz idę już spać

20 lut 23:54
pabel: Dlaczego nie jest prawidlowy? W podstawie ma kwadrat
21 lut 01:03
wredulus_pospolitus:
ostrosłup PRAWIDŁOWY oznacza, że wszystkie ściany boczne tego ostrosłupa są takie same ...
czyli (m.in.) nachylone pod tym samym kątem do podstawy
21 lut 01:28
wredulus_pospolitus:
albo jak wolisz bardziej definicję:
ostrosłup prawidłowy posiada figurę foremna w podstawie, a rzutem jego wierzchołka jest
środek geometryczny podstawy (co oznacza to co napisałem powyżej)
21 lut 01:31
pabel: ok rozumiem
a dlaczego na rysunku kąty między wszystkimi krawędziami bocznymi a podstawą są proste a nie
tylko ta krawędź CD?
21 lut 11:29
wredulus_pospolitus:
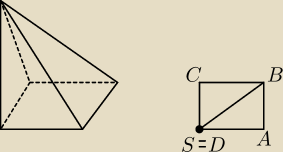
wskaż mi miejsce gdzie jest podane na tym rysunku że kąt nachylenia ściany ABS do podstawy jest
równy 90
o
To samo pytanie dotyczy ściany BCS.
Po lewej rysunek tego ostrosłupa. Po prawej jego RZUT Z GÓRY.
Te wszystkie kąty proste (pomijając te dwa przy punkcie E) właśnie mówią nam o tym, że
wierzchołek S leży 'nad' wierzchołkiem D
21 lut 11:37
pabel: eh popieprzone to jakies
21 lut 12:33
pabel: i jak bede pisal mature to jak ja mam zczaic ze tutaj bedzie kat prosty, tutaj nie... a to
kluczowe w rozwiazywaniu zadan ze stereo
21 lut 12:33
wredulus_pospolitus:
Mamy końcówkę lutego ... jeżeli nie celujesz (a raczej nie celujesz) w 100% z matury to po
prostu na chwilę obecną ODPUŚĆ sobie geometrię i skup się na innych działach matematyki. Jak
je już dobrze opanujesz, wtedy siądź do geometrii i opanuj chociaż podstawy.
21 lut 12:41
Mila:
Już wyjaśniam.
21 lut 16:54
Mila:
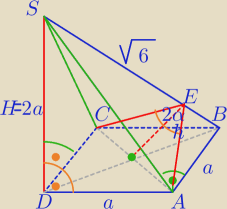
SD⊥do płaszczyzny ABCD− z treści zadania⇔że SD jest prostopadłe do każdej prostej
leżącej w płaszczyźnie ABCD i przechodzącej przez punkt przebicia SD to znaczy pkt. D
Zatem:
1) SD⊥DC, SD⊥DA, SD⊥DB
2) W ΔSDA: z tw. Pitagorasa
|SA|
2=(2a)
2+a
2=5a
2
|SA|=a
√5
2)ΔSDA≡ΔCDS − bkb⇔|SC|=a
√5
3) W ΔSDB: |DB|=a
√2− przekątna kwadratu
|SB|
2=(2a)
2+(a
√2)
2=6a
2
|SB|=a
√6
4) Sprawdzamy jakim trójkątem jest ΔABS− z tw. odwrotnego do tw. Pitagorasa
Boki Δ: a, a
√5, a
√6
(a
√6)
2=? a
2+(a
√5)
2
6a
2=a
2+5a
2 , L=P ⇔ΔABS jest trójkątem prostokątnym,
największy kąt (90
o) leży naprzeciw najdłuższego boku
ΔSCB≡ΔSAB − bbb
5) AE⊥SB i CE⊥SB
|AE|=|CE|− to są wysokości opuszczone z kata prostego na przeciwprostokątną
Teraz pracuj samodzielnie.
21 lut 17:19

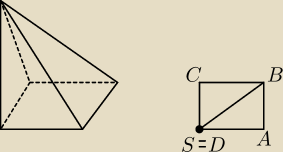 wskaż mi miejsce gdzie jest podane na tym rysunku że kąt nachylenia ściany ABS do podstawy jest
równy 90o
To samo pytanie dotyczy ściany BCS.
Po lewej rysunek tego ostrosłupa. Po prawej jego RZUT Z GÓRY.
Te wszystkie kąty proste (pomijając te dwa przy punkcie E) właśnie mówią nam o tym, że
wierzchołek S leży 'nad' wierzchołkiem D
wskaż mi miejsce gdzie jest podane na tym rysunku że kąt nachylenia ściany ABS do podstawy jest
równy 90o
To samo pytanie dotyczy ściany BCS.
Po lewej rysunek tego ostrosłupa. Po prawej jego RZUT Z GÓRY.
Te wszystkie kąty proste (pomijając te dwa przy punkcie E) właśnie mówią nam o tym, że
wierzchołek S leży 'nad' wierzchołkiem D
 SD⊥do płaszczyzny ABCD− z treści zadania⇔że SD jest prostopadłe do każdej prostej
leżącej w płaszczyźnie ABCD i przechodzącej przez punkt przebicia SD to znaczy pkt. D
Zatem:
1) SD⊥DC, SD⊥DA, SD⊥DB
2) W ΔSDA: z tw. Pitagorasa
|SA|2=(2a)2+a2=5a2
|SA|=a√5
2)ΔSDA≡ΔCDS − bkb⇔|SC|=a√5
3) W ΔSDB: |DB|=a√2− przekątna kwadratu
|SB|2=(2a)2+(a√2)2=6a2
|SB|=a√6
4) Sprawdzamy jakim trójkątem jest ΔABS− z tw. odwrotnego do tw. Pitagorasa
Boki Δ: a, a√5, a√6
(a√6)2=? a2+(a√5)2
6a2=a2+5a2 , L=P ⇔ΔABS jest trójkątem prostokątnym,
największy kąt (90o) leży naprzeciw najdłuższego boku
ΔSCB≡ΔSAB − bbb
5) AE⊥SB i CE⊥SB
|AE|=|CE|− to są wysokości opuszczone z kata prostego na przeciwprostokątną
Teraz pracuj samodzielnie.
SD⊥do płaszczyzny ABCD− z treści zadania⇔że SD jest prostopadłe do każdej prostej
leżącej w płaszczyźnie ABCD i przechodzącej przez punkt przebicia SD to znaczy pkt. D
Zatem:
1) SD⊥DC, SD⊥DA, SD⊥DB
2) W ΔSDA: z tw. Pitagorasa
|SA|2=(2a)2+a2=5a2
|SA|=a√5
2)ΔSDA≡ΔCDS − bkb⇔|SC|=a√5
3) W ΔSDB: |DB|=a√2− przekątna kwadratu
|SB|2=(2a)2+(a√2)2=6a2
|SB|=a√6
4) Sprawdzamy jakim trójkątem jest ΔABS− z tw. odwrotnego do tw. Pitagorasa
Boki Δ: a, a√5, a√6
(a√6)2=? a2+(a√5)2
6a2=a2+5a2 , L=P ⇔ΔABS jest trójkątem prostokątnym,
największy kąt (90o) leży naprzeciw najdłuższego boku
ΔSCB≡ΔSAB − bbb
5) AE⊥SB i CE⊥SB
|AE|=|CE|− to są wysokości opuszczone z kata prostego na przeciwprostokątną
Teraz pracuj samodzielnie.