geometria analityczna, trójkąty
kasiaba: Podstawa AB trójkąta równoramiennego ABC zawarta jest w prostej x + y + 1 = 0. Ramię BC zawiera
się w prostej 2x − y−1 =0 . Wyznacz równanie prostej k zawierającej ramię AC wiedząc, że punkt
P = (−4,0) należy do prostej k. Zrobiłam rysunek i obliczyłam, że B=(0,−1). Co dalej?
20 lut 12:59
Tadeusz:
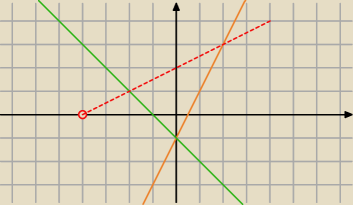
20 lut 14:52
janek191:
Poprowadź przez P = ( − 4, 0) prostą równoległą do prostej AB ( y = − x − 1 )
Znajdź punkt wspólny R tej prostej i prostej BC ( y = 2 x − 1)
R = ( − 1 , − 3) )
I PC I = I RC I
C = ( x, 2 x − 1)
C = ( 2, 3)
========
20 lut 15:03
6latek: Czesc
janek191 
A jak bym chcial zrobic tak (rysunek Tadka )
1) Wyznaczam kat miedzy zielona a pomaranczowa
2) Pisze rownanie prostej przechodzacej przez punkt P i przecinajaca zielona pod kątem
wyznaczonym w punkcie nr 1
Chodzi mi bardziej o punkt nr 2 Jakby to rownanie mialoby wygladac w postaci ogolnej
Tzn np rownanie prostej przechodzacej przez dany punkt jest takie
y=m(x−x
0)+y
0
Czxy za m wstawic ten kąt wyliczony w punkcie 1?
20 lut 15:20
6latek: Zapomnialem

20 lut 15:23
6latek:
20 lut 16:31
6latek: Ponawiam pytanie .
20 lut 19:24
Tadeusz:
Sądziłem, że już "zgryzłeś"
Małolacie 
20 lut 19:26
6latek: Dobry wieczor

Nie mialem czasu zobaczyc
20 lut 19:27
Tadeusz:
| | a1−a2 | |
tgα=| |
| | (kąt ostry między prostymi) |
| | 1+a1*a2 | |
Dla dwóch danych prostych otrzymasz tgα=3
To teraz poszukaj współczynnika kierunkowego prostej (a
3} przy którym kąt z prostą
y=−x−1 jest taki ze jego tangens jest równy 3
| | a3+1 | |
3=| |
| | dostaniesz a3=1/2 lub a3=2 |
| | 1−a3 | |
| | 1 | | 1 | |
Zatem prosta zawierająca AC y−0= |
| (x+4) ⇒ y= |
| x+2 |
| | 2 | | 2 | |
20 lut 19:48
6latek: O .Dobrze

20 lut 19:57

 A jak bym chcial zrobic tak (rysunek Tadka )
1) Wyznaczam kat miedzy zielona a pomaranczowa
2) Pisze rownanie prostej przechodzacej przez punkt P i przecinajaca zielona pod kątem
wyznaczonym w punkcie nr 1
Chodzi mi bardziej o punkt nr 2 Jakby to rownanie mialoby wygladac w postaci ogolnej
Tzn np rownanie prostej przechodzacej przez dany punkt jest takie
y=m(x−x0)+y0
Czxy za m wstawic ten kąt wyliczony w punkcie 1?
A jak bym chcial zrobic tak (rysunek Tadka )
1) Wyznaczam kat miedzy zielona a pomaranczowa
2) Pisze rownanie prostej przechodzacej przez punkt P i przecinajaca zielona pod kątem
wyznaczonym w punkcie nr 1
Chodzi mi bardziej o punkt nr 2 Jakby to rownanie mialoby wygladac w postaci ogolnej
Tzn np rownanie prostej przechodzacej przez dany punkt jest takie
y=m(x−x0)+y0
Czxy za m wstawic ten kąt wyliczony w punkcie 1?


 Nie mialem czasu zobaczyc
Nie mialem czasu zobaczyc
