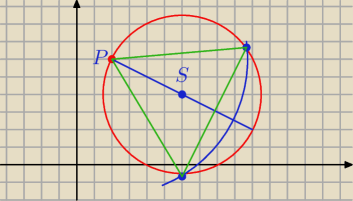
W okrąg wpisano trójkąt równoboczny 100onmywrist: W okrąg o równaniu x² +y² −12x −8y +32 =0 wpisano trójkąt równoboczny, którego jednym z wierzchołków jest punkt p(2,6). Wyznacz pozostałe boki tego trójkąta Przekształciłem równanie okręgu i wznaczam z niego środek S(6,4) oraz promień r=2√5. Skorzystałem ze wzoru, że R=2/3H, wyliczyłem, że h =3√5, a=2√15, tu się zaczynają schody, kombinowałem i wyznaczyłem prostą przechodzącą przez punkt O i S i na pewno przez punkt A który jest środkiem przeciwległego boku y =−1/2x+7 i podstawiłem to jako współrzędną Y we wzorze na długość odcinka PA. wychodzą niemiłe wyniki, więc z góry zakładam, że to źle. jakies wsazówki?

janek191: ( x − 6)² − 36 + ( y − 4)² − 16 + 32 = 0 (x − 6)² + ( y − 4)² = 4*5 S = ( 6, 4) r = 2√5 h = 3√5 a = 2√15 ( x − 2)² + ( y − 6)² = 60 Rozwiązuję układ: x² + y² − 12 x − 8 y + 32 = 0 x² − 4 x + 4 + y² − 12 y + 36 = 60 −−−−−−−−−−−−−−−− odejmuję stronami 2 x − y = 13 y = 2 x − 13 x² − 16 x + 61 = 0 Δ = 12 x₁ = 8 − √3 y₁ = 3 − 2 √3 x₂ = 8 + √3 y₂ = 3 + 2√3

janek191: ( x − 2)² + ( y − 6)² = a² = 60 − równanie okręgu o środku P = ( 2, 6) i promieniu a = 2√15