fggd
Laufer:
Witam,
Dobrze to rozwiązałem?
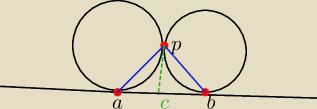
Dwa okręgi są styczne zewnętrznie w punkcie P. Poprowadzono styczną do obu okręgów odpowiednio
w punktach
A i B. Wykaż, że kąt APB jest prosty
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
Jeżeli poprowadzimy odcinek |PC|, to wówczas |AC|=|PC|=|CB|=R. Czyli jest to trójkąt
prostokątny,
gdzie R jest promieniem okręgu opisanego na tym trójkącie.
Może być?
19 lut 09:39
Jerzy:
Nie może. Gdzie jest napisane,że okręgi maja taki sam promień ?
19 lut 09:58
Laufer: Nie założyłem tak. Nie jest prawdą, że |AC|=|PC|=|CB|? Przecież są to odcinki powstałe
z przecięcia prostych przechodzących przez punkty styczności. Więc muszą być równe

19 lut 10:47
Jerzy:
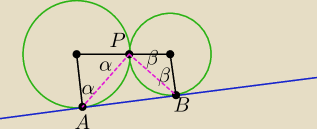
Kąt APB = 180 − (x + y) , gdzie x i y to katy pomiedzy cięciwami i styczną
Mamy: x = 90 − α i y = 90 − β
Czyli : kąt APB = 180 − [(90 − α) + (90 − β)] = α + β
Dalej mamy: (α + β) + (α +β)β = 180 ⇔ 2(α + β) =180 ⇔ α + β = 90 cnw.
19 lut 11:30
Jerzy:
Ostatnia linijka: (α + β) + (α + β) = 180 ⇔ 2(α + β) = 180 ⇔ α + β = 90 cnw.
19 lut 11:40
PW: Jerzy, właśnie miałem rysować ten trapez, ale nie zdążyłem, bo zacząłem się zastanawiać
czy uczeń wie, że prosta przechodząca przez środki okręgów zawiera punkt styczności P. Jest to
istotne w tym zadaniu, powinno się to wyraźnie napisać, a nie wiem czy jest takie twierdzenie
w szkole, czy też uznać to za fakt oczywisty.

19 lut 11:49
Pytający:
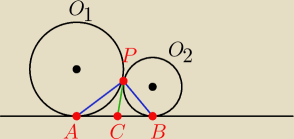
Analizując to co napisał
Laufer.
Dorysujmy prostą PC taką, żeby była ona styczna od okręgów O
1 i O
2 w punkcie P.
Wówczas dla okręgu O
1 mamy, że |AC|=|PC| (z tw. o stycznych do okręgu)
Analogicznie dla okręgu O
2 mamy, że |BC|=|PC|, zatem
|AC| = |BC| = |PC|. Oznacza to, że punkt C jest środkiem okręgu opisanego na trójkącie ABP
(jest równoodległy od każdego wierzchołka trójkąta).
Zauważmy, że AB jest średnicą okręgu opisanego na trójkącie ABP, wobec tego
kąt APB jest oparty na średnicy, czyli jest to kąt prosty.
Wobec tego trójkąt ABP jest prostokątny.
19 lut 12:45
PW: No właśnie tego brakło Laufrowi w jego opisie − co to za odcinek PC.
Tu również zastanawiam się − czy jest oczywiste, że styczna w punkcie P do jednego z okręgów
jest styczną do drugiego. Uznać to za oczywiste, bo tak narysowano, czy jakoś uzasadnić?
Matematycy w takiej sytuacji zwykli pisać: "Jest oczywiste że ...". Jestem ciekawy, czy
Laufer podałby zgrabne usasadnienie.
19 lut 13:45
 Witam,
Dobrze to rozwiązałem?
Dwa okręgi są styczne zewnętrznie w punkcie P. Poprowadzono styczną do obu okręgów odpowiednio
w punktach
A i B. Wykaż, że kąt APB jest prosty
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
Jeżeli poprowadzimy odcinek |PC|, to wówczas |AC|=|PC|=|CB|=R. Czyli jest to trójkąt
prostokątny,
gdzie R jest promieniem okręgu opisanego na tym trójkącie.
Może być?
Witam,
Dobrze to rozwiązałem?
Dwa okręgi są styczne zewnętrznie w punkcie P. Poprowadzono styczną do obu okręgów odpowiednio
w punktach
A i B. Wykaż, że kąt APB jest prosty
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
Jeżeli poprowadzimy odcinek |PC|, to wówczas |AC|=|PC|=|CB|=R. Czyli jest to trójkąt
prostokątny,
gdzie R jest promieniem okręgu opisanego na tym trójkącie.
Może być?

 Kąt APB = 180 − (x + y) , gdzie x i y to katy pomiedzy cięciwami i styczną
Mamy: x = 90 − α i y = 90 − β
Czyli : kąt APB = 180 − [(90 − α) + (90 − β)] = α + β
Dalej mamy: (α + β) + (α +β)β = 180 ⇔ 2(α + β) =180 ⇔ α + β = 90 cnw.
Kąt APB = 180 − (x + y) , gdzie x i y to katy pomiedzy cięciwami i styczną
Mamy: x = 90 − α i y = 90 − β
Czyli : kąt APB = 180 − [(90 − α) + (90 − β)] = α + β
Dalej mamy: (α + β) + (α +β)β = 180 ⇔ 2(α + β) =180 ⇔ α + β = 90 cnw.

 Analizując to co napisał Laufer.
Dorysujmy prostą PC taką, żeby była ona styczna od okręgów O1 i O2 w punkcie P.
Wówczas dla okręgu O1 mamy, że |AC|=|PC| (z tw. o stycznych do okręgu)
Analogicznie dla okręgu O2 mamy, że |BC|=|PC|, zatem
|AC| = |BC| = |PC|. Oznacza to, że punkt C jest środkiem okręgu opisanego na trójkącie ABP
(jest równoodległy od każdego wierzchołka trójkąta).
Zauważmy, że AB jest średnicą okręgu opisanego na trójkącie ABP, wobec tego
kąt APB jest oparty na średnicy, czyli jest to kąt prosty.
Wobec tego trójkąt ABP jest prostokątny.
Analizując to co napisał Laufer.
Dorysujmy prostą PC taką, żeby była ona styczna od okręgów O1 i O2 w punkcie P.
Wówczas dla okręgu O1 mamy, że |AC|=|PC| (z tw. o stycznych do okręgu)
Analogicznie dla okręgu O2 mamy, że |BC|=|PC|, zatem
|AC| = |BC| = |PC|. Oznacza to, że punkt C jest środkiem okręgu opisanego na trójkącie ABP
(jest równoodległy od każdego wierzchołka trójkąta).
Zauważmy, że AB jest średnicą okręgu opisanego na trójkącie ABP, wobec tego
kąt APB jest oparty na średnicy, czyli jest to kąt prosty.
Wobec tego trójkąt ABP jest prostokątny.