Oblicz granicę ciągu.
Kam:

x→nieskończoności
Wydaje mi się, że x
2−4 powinienem zamienić na (x−2)(x+2), natomiast dalej nie mam pomysłu.
Kluczowe jest prawdopodobnie teraz ile to
√x, a więc ile to jest
√nieskończoność
Proszę o wytłumaczenie, a także rozwiązanie zadania

18 lut 21:30
iteRacj@:
Kluczowe jest to, czy licznik i mianownik rosną i który szybciej.
Wiemy, że skoro x→
∞ to również
√x→
∞.
x dążąc do nieskończoności, przyjmuje wartości dodatnie, więc
| | √x+5 | | √x+5 | |
limx→∞ |
| = limx→∞ |
| = |
| | x2−4 | | (√x)4−4 | |
18 lut 22:26
Kam:
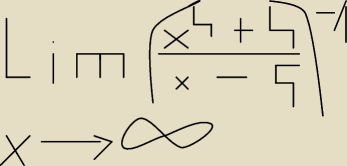
Dziękuje serdecznie za pomoc. Tak więc skoro mam odpowiedzi sugerowane:
A) jest równa 0
B) nie istnieje
C) jest równa granicy (patrz rysunek)
D) jest równa −5/4
Tak więc na pewno poprawna jest A, natomiast na pewno nie poprawna B,D.
Co w przypadku C?
19 lut 15:21
konrad: A czy jest to test wielokrotnego wyboru? Bo ta druga granica też wynosi 0.
19 lut 15:36
iteRacj@:
dla (x→
∞) w tym wyrażeniu również mianownik rośnie szybciej
| | x4+4 | | x−5 | |
więc ( |
| )−1= |
| → 0 |
| | x−5 | | x4+4 | |
czyli odpowiedzi A i C
19 lut 17:59
Kam: Tak, pytanie jest wielokrotnego wyboru

19 lut 20:51


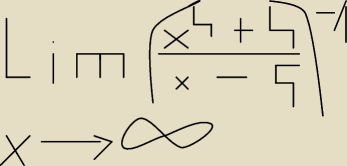 Dziękuje serdecznie za pomoc. Tak więc skoro mam odpowiedzi sugerowane:
A) jest równa 0
B) nie istnieje
C) jest równa granicy (patrz rysunek)
D) jest równa −5/4
Tak więc na pewno poprawna jest A, natomiast na pewno nie poprawna B,D.
Co w przypadku C?
Dziękuje serdecznie za pomoc. Tak więc skoro mam odpowiedzi sugerowane:
A) jest równa 0
B) nie istnieje
C) jest równa granicy (patrz rysunek)
D) jest równa −5/4
Tak więc na pewno poprawna jest A, natomiast na pewno nie poprawna B,D.
Co w przypadku C?
