W graniastosłupie
ET:
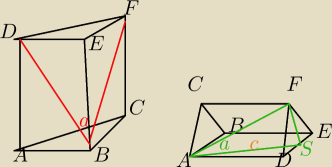
W graniastosłupie prawidłowym trójkątnym pole powierzchni bocznej równa się sumie pól obu
podstaw. Oblicz tangens kąta nachylenia przekątnej ściany bocznej do sąsiedniej ściany
bocznej.
Dlaczego pierwszy rysunek w tym zadaniu nie jest poprawny?W sensie wiem,że w poleceniu nie ma
'kąta między przękatnymi sąsiednich ścian bocznych',ale skąd wiemy,że ten bok c dzieli bok DE
na pół,co za tym idzie |DS|=|DE|?
iteRacj@:
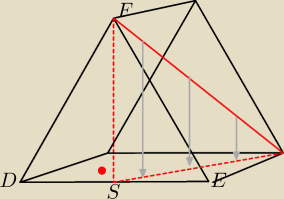
widok "z góry"
W graniastosłupie prawidłowym trójkątnym podstawy są trójkątami równobocznymi.
Kąt nachylenia przekątnej ściany bocznej do sąsiedniej ściany bocznej wyznacza trójkąt o
wierzchołkach: B, F i rzut prostokątny F na bok DE czyli pkt S. Jest on środkiem boku DE stąd
|DS|=|SE|.
 W graniastosłupie prawidłowym trójkątnym pole powierzchni bocznej równa się sumie pól obu
podstaw. Oblicz tangens kąta nachylenia przekątnej ściany bocznej do sąsiedniej ściany
bocznej.
Dlaczego pierwszy rysunek w tym zadaniu nie jest poprawny?W sensie wiem,że w poleceniu nie ma
'kąta między przękatnymi sąsiednich ścian bocznych',ale skąd wiemy,że ten bok c dzieli bok DE
na pół,co za tym idzie |DS|=|DE|?
W graniastosłupie prawidłowym trójkątnym pole powierzchni bocznej równa się sumie pól obu
podstaw. Oblicz tangens kąta nachylenia przekątnej ściany bocznej do sąsiedniej ściany
bocznej.
Dlaczego pierwszy rysunek w tym zadaniu nie jest poprawny?W sensie wiem,że w poleceniu nie ma
'kąta między przękatnymi sąsiednich ścian bocznych',ale skąd wiemy,że ten bok c dzieli bok DE
na pół,co za tym idzie |DS|=|DE|?
 widok "z góry"
W graniastosłupie prawidłowym trójkątnym podstawy są trójkątami równobocznymi.
Kąt nachylenia przekątnej ściany bocznej do sąsiedniej ściany bocznej wyznacza trójkąt o
wierzchołkach: B, F i rzut prostokątny F na bok DE czyli pkt S. Jest on środkiem boku DE stąd
|DS|=|SE|.
widok "z góry"
W graniastosłupie prawidłowym trójkątnym podstawy są trójkątami równobocznymi.
Kąt nachylenia przekątnej ściany bocznej do sąsiedniej ściany bocznej wyznacza trójkąt o
wierzchołkach: B, F i rzut prostokątny F na bok DE czyli pkt S. Jest on środkiem boku DE stąd
|DS|=|SE|.