punkt symetryczny do prostej w postaci parametrycznej
x: Znaleźć punkt symetryczny do punktu K(1,3,1) względem prostej
l: x = 1, y = 1 − t, z = 3 + 2t
17 lut 11:08
ABC:
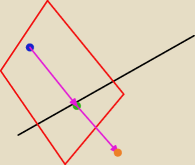
poprowadź płaszczyznę prostopadła do prostej przez ten punkt K, znajdź punkt przebicia
płaszczyzny przez prostą, zbuduj wektor i wydłuż go dwukrotnie
17 lut 11:19
x: czyli?− możesz dać w skrócie jakieś instrukcje?− dzięki
17 lut 11:22
Jerzy:
Wektor kierunkowy danej prostej jest wektorem normalnym tej płaszczyzny.
17 lut 11:24
ABC: dobrze ci Jerzy podpowiada , wektor kierunkowy prostej to (0,−1,2)
równanie płaszczyzny o wektorze normalnym (A,B,C) przechodzącej przez punkt (x
0, y
0, z
0)
znasz?
17 lut 11:34
x: niestety nie
17 lut 13:33
Jerzy:
A(x − x0) + B(y − y0) + C(z − z0) = 0
17 lut 13:34
x: ok, dzięki − już powinienem dać radę
17 lut 13:36
x: Ale jeszcze jedno − jak znaleźć punkt przebicia płaszczyzny przez prostą?
17 lut 13:43
Jerzy:
Do równania płaszczyzny podstawiasz równanie parametryczne prostej i obliczasz t.
17 lut 13:45