Okrąg opisany na trójkącie, kąty, planimetria
kasiaba: Dwusieczne kątów A i B trójkąta ABC przecinają okrąg opisany na nim odpowiednio w punktach K i
L. Oblicz miary katów czworokąta ABKL wiedząc, że kąt BAC = 60 st i kąt ABC = 40 st.
Prosiłabym o rozwiązanie zadania od początku do końca, ponieważ nie wiem, gdzie mam błąd i nie
mogę go znaleźć

iteRacj@:
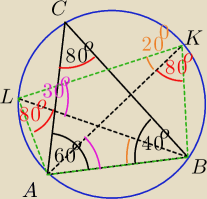
|<LKA|=|<LBA|=1/2*|<ABC|=20
o
|<KLB|=|<KAB|=1/2*|<CAB|=30
o
|<AKB|=|<ALB|=|<ACB|=180
o−60
o−40
o=80
o
Korzystam z twierdzeń o kątach wpisanych opartych na tym samym łuku i o sumie kątów czworokąta
wpisaneo w okrąg.
|<LKB|=80
o+20
o=100
o → |<LAB|=180
o−|<LKB|=80
o
|<KLA|=80
o+30
o=110
o → |<ABK|=180
o−|<KLA|=70
o

 |<LKA|=|<LBA|=1/2*|<ABC|=20o
|<KLB|=|<KAB|=1/2*|<CAB|=30o
|<AKB|=|<ALB|=|<ACB|=180o−60o−40o=80o
Korzystam z twierdzeń o kątach wpisanych opartych na tym samym łuku i o sumie kątów czworokąta
wpisaneo w okrąg.
|<LKB|=80o+20o=100o → |<LAB|=180o−|<LKB|=80o
|<KLA|=80o+30o=110o → |<ABK|=180o−|<KLA|=70o
|<LKA|=|<LBA|=1/2*|<ABC|=20o
|<KLB|=|<KAB|=1/2*|<CAB|=30o
|<AKB|=|<ALB|=|<ACB|=180o−60o−40o=80o
Korzystam z twierdzeń o kątach wpisanych opartych na tym samym łuku i o sumie kątów czworokąta
wpisaneo w okrąg.
|<LKB|=80o+20o=100o → |<LAB|=180o−|<LKB|=80o
|<KLA|=80o+30o=110o → |<ABK|=180o−|<KLA|=70o