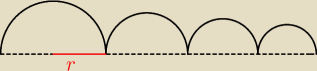
polokregi safasfasf: Z półokręgów budujemy krzywą. Pierwszy półokrąg ma promień długości r,r > 0 , a promień każdego

	2
następnego półokręgu stanowi		promienia poprzedniego. Niech n oznacza liczbę półokręgów
	3

tworzących tę krzywą. Udowodnij, że dla dowolnej liczby naturalnej dodatniej n długość krzywej jest mniejsza od 3πr więc a₁=πr

	2
q=
	3

|q|<1,spełnia założenie

	πr
S=		=3πr,co tu jest źle?w takim razie nie jest mniejsza od 3πr a ma być mniejsza
	1   3

ABC: ty policzyłeś granicę , a w poleceniu masz "dla dowolnej liczby naturalnej" , dowolnej ale ustalonej, na przykład 1000