Suriekcja
Krzysztof: Funkcja "na", jak prawidłowo to wyjaśnić?
Które z podanych funkcji są "na". Dlaczego?
a) f: R −> (0, ∞), f(x) = x2
b) g: [0, 2π) −> [−1,1], g(x) = sinx
15 lut 19:12
Franciszek : Dołączam się do pytania
15 lut 19:20
Wish you were here: f: X→Y jest typu na jesli
⋀ y∊Y ⋁x∊X y=f(x)
Odwzorowanie jest ty[pu na jesli dla dowolnego wybranego elementu y∊Y uda sie znalezc w
zbiorze X taki element x ze (x) przechpdzi na (y) przy odwzorowaniu f
15 lut 19:26
janek191:
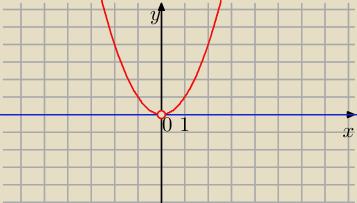
a) f : ℛ → ( 0, +
∞)
Pewnie nie jest na , bo f(0) ∉ ( 0, +
∞)
15 lut 21:01
janek191:
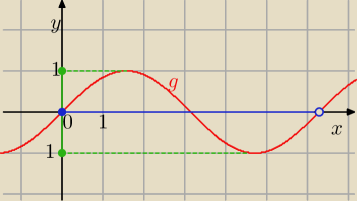
Funkcja g: < 0, 2π ) → < −1, 1> jest "na"
g(x) = sin x
15 lut 21:09
Adamm:
f:R→(0, ∞), f(x) = x2
wydaje mi się że to nie jest nawet prawidłowa definicja funkcji
15 lut 21:16
janek191:
Tak, bo nie każdemu elementowi x ∊ ℛ przyporządkowano f(x) .
15 lut 21:20
 a) f : ℛ → ( 0, +∞)
Pewnie nie jest na , bo f(0) ∉ ( 0, +∞)
a) f : ℛ → ( 0, +∞)
Pewnie nie jest na , bo f(0) ∉ ( 0, +∞)
 Funkcja g: < 0, 2π ) → < −1, 1> jest "na"
g(x) = sin x
Funkcja g: < 0, 2π ) → < −1, 1> jest "na"
g(x) = sin x