. anx: W kulę o promieniu 6cm wpisano ostrosłup prawidłowy trójkątny o największej objętości. Wykaż, że ostrosłup ten jest czworoscianem foremnym, którego krawędź ma długość 4√6cm. Czy ktoś mógłby podpowiedzieć, jak to w ogóle rozrysować? Bardzo proszę

anx: .

anx: .

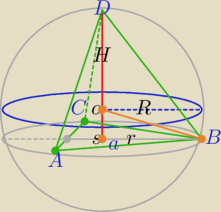
Mila: R=6cm, H=|SD|

	1
V=		*PΔABC*H
	3

1) |OS|=x, H=6+x, x=H−6 |OB|=R=6 r− promień małego koła (opisanego na Δrównobocznym, o boku a)

	2		a√3
r=		hΔ=
	3		3

W ΔBSO: R²=x²+r² x²+r²=36

	a√3
(H−6)2+(		)2=36
	3

a²=3*(12H−H²) ( 6<H<12) 2) Optymalizacja

	1		a2√3
V=		*		*H
	3		4

	1		1		√3
V(H)=		*		*3(12H−H2 )√3*H=		*(12H2−H3)
	3		4		4

	√3
V'(H)=		*(24H−3H2)
	4

V'(H)=0 H=0∉D lub H=8 Dla H=8 funkcja V(H) osiąga wartość największą ( wiesz dlaczego?, wyjaśnij sama) a²=3*(12*8−64) a²=96=16*6 a=4√6 Sama sprawdź długość krawędzi bocznej

anx: Dziękuję bardzo!