Całka W.: Jak obliczyc całkę: ∫ (√4−x²−1) dx Proszę o pomoc

wredulus_pospolitus: ∫√4−x² dx − ∫ dx druga −−− banał pierwsza −−− przez części: u' = 1 ; v = √4−x²

W.: A jeśli obliczam ją w granicach −pierwiastek{3} do pierwiastek{3} to później po podstawieniu wychodzi całka od 1 do 1. Czy to ma sens?

W.: Chodzi mi o podstawienie w liczeniu tej pierwszej całki, przy calkowaniu przez części

Mariusz: wredulus napisał ci jak masz dobrać części Po scałkowaniu przez części korzystasz z tego że

	4−x2
√4−x2=
	√4−x2

Obliczając u z u'=1 tutaj możesz przyjąć że stała C= 0 Całkując przez podstawienie zmieniasz przedział całkowania Całkując przez części nie zmieniasz przedziału całkowania

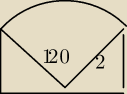
jc: Całka z zadania to pole figury z rysunku = 4π/3 + √3 (na rysunku jest oczywiście zły kąt)

Bleee: Przecież funkcja podcalkowa jest funkcja parzysta... Więc dla takich granic calkowania wynikiem bedzie 0 (bez liczenia samej całki). Chyba że jest inne polecenie, czyli nie: "oblicz calke oznaczona"

Bleee: Tfuuuu... Co za głupotę walnalem Toc dla nieparzyste mielibyśmy 0