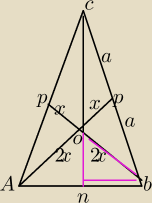
geometria pytanie kama: Nie chcę rozwiązania do tego zadania mam tylko jedno pytanie: W trójkącie ABC, gdzie AC=BC=2a środkowe poprowadzone z wierzchołków A i B przecinają się pod kątem prostym.

	6a2
Wykaż, że pole trójkąta ABC jest równe P=
	5

Zrobiłam rysunek podstawa b, ramiona a, środkowe przecinają się w stosunku 1:2 zrobiłam wychodząc z rysunku trójkąta ABP, ale jak próbowałam wyjść z trójkąta NOB (różowy) to zadanie nie wyszło. I tego nie rozumiem, bo wychodzi na to, że odcinek CN nie jest podzielony w stosunku 1:2 przecież ta wysokość jest jednocześnie środkową−dlaczego ? Dobre rozwiązanie wyszło mi tak: x²+4x²=a² a²=√5x

	a√5
x=
	5

(CN)²=4a²−(x√2)²

	3a√10
CN=		podstawiłam do wzoru na pole trójkąta i wyszło, ale jak wyszłam z tego
	5

trójkąta różowego czyli podstawa to b NO=x i pitagoras itd. to nie wychodzi, tak jakby odcinek CN nie był środkową, i nie mogłabym użyć tego, że NO=x a OC= 2x czego tu nie widzę i nie rozumiem, proszę tylko to mi wyjaśnić, jeśli rozumiecie o co pytam.

wredulus_pospolitus: Wychodząc z ΔNOB dlaczego |NO| = x Zauważ, że |NO| to wysokość trójkąta równoramiennego o kącie podstawy 45^o

wredulus_pospolitus: albo jak wolisz −−− |NO| to połowa przekątnej kwadratu o boku 2x

kama: ale czy NO nie jest też środkową ?

kama: Nikt nie pomoże ?

Mila: Dwie środkowe poprowadzone z wierzchołków A i B są równe, środkowa CN ma inną długość. |NO|=y i |OC|=2y

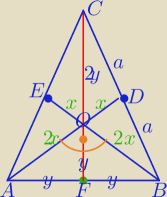
Mila: 1) W ΔBOD: a²=x²+(2x)² ⇔a²=5x²

	a2
x2=
	5

======= 2) |AB|=2x√2 − jako przekątna kwadratu y=x√2

	1		a2
PΔBFO=		*y2=x2=
	2		5

3)

1		a2
	PΔABC=
6		5

	6a2
PΔABC=
	5

cnw ===========

kama: Milu niepotrzebnie to robiłaś, ale oczywiście WIELKIE DZIĘKI , wiem o czym źle myślałam .... zrównałam wszystkie środkowe na zasadzie, że ten y=x co za głupota. Dziękuję

Mila: Podałam inny sposób, skorzystaj przy okazji.