Pokaż że pole trójkąta DEF stanowi 12/49 pola trójkąta ABC Dwite: W trójkącie ABC punkt D należy do boku AB, a punkt E do boku AC i zachodzą proporcje |AD| : |DB| = 2 : 7 |AE| : |EC| = 4 : 3. Prosta k jest równoległa do boku AB, przechodzi przez punkt E i przecina bok BC w punkcie F. Pokaż że pole trójkąta

	12
DEF stanowi		pola trójkąta ABC.
	49

Eta:

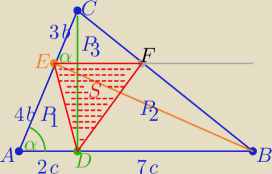
	7b*9c*sinα		63
P(ABC)=P=		=
	2		2

	3
ΔEFC podobny do ΔABC (z cechy (kkk) w skali k=
	7

	9		81
to P(EFC)=P3=		P=		bcsinα
	49		14

	1
P(ADE)=P1=		*4b*2c*sinα = 4bcsinα
	2

	7
P(DBF)= P2=		*P1= 14bcsinα
	2

	54
S=P1+P2+P3=		bcsinα
	7

S		54		2		12
	=		*		=
P		7		63		49

	12
S=		P
	49

========== c.n.w.

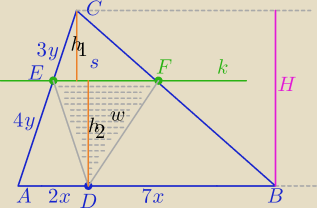Mila: Dołączam II sposób P− pole ΔABC

	3
1)ΔEFC∼ΔABC w skali k=		⇔
	7

	9
PEFC=		P=s
	49

h1		3		3		4
	=		⇔h1=		H i h2=		H
H		7		7		7

2)ΔEFC i ΔEFD mają wspólną podstawę stosunek pół jest równy stosunkowi wysokości:

s		h1		s		3		4
	=		⇔		=		⇔w=		s
w		h2		w		4		3

	4		9
w=		*		P
	3		49

	12
PΔEFD=		P
	49

=============

Dwite: Dzięki !