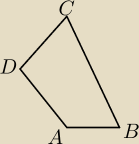Rozważamy wszystkie czworokąty wypukłe ABCD w których
suma długości odcinków AB i BC jest równa 6 , I AD I = I DC I ,
odległość punktu D od przekątnej AC jest równa 1,5 oraz kąt BAC jest prosty.
Oblicz cosinus kąta BCD w tym z rozważanych czworokątów który ma największe pole