. sylwiaczek: oblicz sume piecdziesieciu najmniejszych dodatnich rozwiazan rownania 2sin⁴x = 3sin² −1 wychodzi z tego sinx=1 lub sinx= −1 lub sinx= √2/2 lub sinx = −√2/2 czyli x= π/4+kπ/4 lub x= π/2 + kπ czyli a1= π/4 a2= π/2 a3=3π/4 a4= 5π/4 czyli tutaj juz sie nie zgadza ciag, jak to rozwiazac?

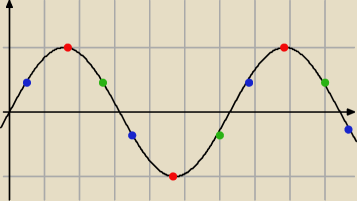
wredulus_pospolitus: robisz trzy ciągi: a_n b_n c_n one 'w sumie' nie dadzą Ci ciągu arytmetycznego ... ale każdy z nich (z osobna) jest arytmetyczny.

sylwiaczek: nie wychodzi mi... robie tak: an: S17 bn: S17 cn: S16 bo 17+17+16=50 no i te sumy dodaje ale to chyba zle bo nie taki wynik

Mila: Jaką masz odpowiedź do zadania?

Mila: Rozpisałam tak, że zrozumiesz. Można mniej ciągów ustalić, ale to jest łopatologicznie.

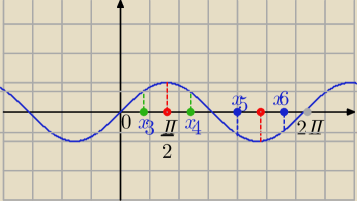
Mila: 1) x>0 sinx=1 lub sin x=−1

	π		3π
x=		+2kπ lub x=		+2kπ
	2		2

	√2		√2
lub sinx=		lub sinx=−
	2		2

2) Jest 6 rozwiązań w przedziale (0,2π): 6*8=48−rozwiązań, i jeszcze dwa rozwiązania z następnego przedziału 3)a_n: 9 wyrazów

	π		π
a1=x3=		, a2=		+2π, r=2π
	4		4

	π		π4+1614π		297π
a9=		+8*2π=1614π, S9=		*9=		=74π14
	4		2		4

4)b_n− 9 wyrazów

	π		π		1
b1=		, r=2π, b9=		+8*2π=16		π
	2		2		2

	1   π2+16 π   2		153π
S9=		*9=
	2		2

5) c_n− 8 wyrazów

	3π		3		3   3π4+14 π   4
c1=x4=		, r=2π, c8=14		π, S8=		*8=62π
	4		4		2

6) d_n− 8 wyrazów

	5π		5π4+1514π
d1=		, r=2π, d8=1514π, S8=		*8=66π
	4		2

7) f_n:

	3π		3π2+1512π
f1=		, f8=1512π, s8=		*8=68π
	2		2

8) g_n

	7π		7π4+1534π
g1=		, g8=1534π, s8=		*8=70π
	4		2

suma =416³₄π