Udowodnij że wykres funkcji przecina os X Dwite: Udowodnij że wykres funkcji f(x) = x³ − x² + x − 6 określonej dla wszystkich x należących do liczb rzeczywistych przecina oś 0X dokładne w jednym punkcie. Oblicz równanie prostej stycznej do wkuresu funkcji f w tym punkcie.

janek191: f '(x) = 3 x² − 2 x + 1 > 0 − f rośnie w ℛ Δ = 4 − 4*3*1 < 0 f(2) = 0 itd.

janek191: Oraz f(0) = − 6 i f(3) = 27 − 9 + 3 − 6 > 0

Dwite: Czyli ten punkt przecinający ox to punkt o współrzędnych (2,0) tak ?

janek191: Tak

Dwite: potem liczyć f'(2) = 9 = a podstawić punkt (2,0) do y=9x+b zatem b = −18 a równanie prostej to y=9x−18 Dobrze czy cos robie źle ?

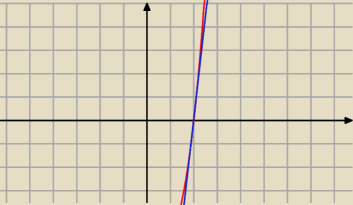
janek191: Dobrze

Dwite: super, dzięki za pomoc !