. sylwiaczek: oblicz sume stu poczatkowych wyrazow ciagu an, n≥1 an= ncos(nπ)

Mila: Jakie próby podjęłaś?

Mila:

sylwiaczek: nie wiem co zrobic z 100cos100π

sylwiaczek: czyli cos100π bedzie 1?

ABC: tak

Mila: 1) Wypisz kilka wyrazów ciągu a_n o nieparzystych numerach a₁,a₃,a₅, .... 2) Wypisz kilka wyrazów ciągu a_n o parzystych numerach a₂, a₄,a₆,... a₁₀₀=100*1=100 3) Zauważysz pewną prawidłowość.

sylwiaczek:

	cosπ + 100cos100π
to by wychodzilo S100 =		* 100= 99 * 50 a to zle
	2

ABC: Sylwiaczek wypisz sobie kilkanaście początkowcyh wyrazów

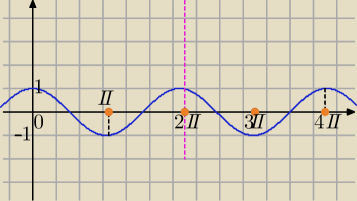
Mila: Popatrz na wykres, co tam widzisz? Jaką wartość ma cosinus dla, π, 3π ? I wypisz te początkowe wyrazy, tu na forum, tak jak podpowiedziałam.

sylwiaczek: to wychodzi : −1 +2 −3 +4 −5 +... czyli to jest szereg? ale jakie q?

sylwiaczek: aa dobra, wiem

sylwiaczek: a nie, jednak nwm, jak to dalej?

Mila: Żadne q, tu nie ma ciągu geometrycznego. 1)Wyrazy o nieparzystych numerach: a₁=−1 a₂=−3 a₃=−5 Ciąg arytmetyczny a₁=−1, r=−2 Liczba wyrazów :50 (wiesz dlaczego?) a₉9=−1+(50−1)*(−2)=−1−98=−99

	−1−99		−100
S=		*50=		*50==−2500
	2		2

2) Wyrazy o parzystych numerach: b₁=a₂=2 b₂=a₄=4 b₃=a₆=6 Ciąg arytmetyczny: b₁=2, r=2 Liczba wyrazów : 50

	a2+a100
S=		*50
	2

dokończ

sylwiaczek: dziekuje!

Mila: Jaką masz sumę?

Mariusz: Mila może i tu nie ma ciągu geometrycznego ale funkcja tworząca tego ciągu jest pochodną szeregu geometrycznego

	1
∑(−1)nxn=
	1+x

d		d		1
	(∑(−1)nxn)=		(		)
dx		dx		1+x

	1
∑n(−1)nxn−1=−
	(1+x)2

	x
∑n(−1)nxn=−
	(1+x)2

Funkcję tworzącą ciągu sum częściowych łatwo otrzymać układając równanie rekurencyjne

	x
S(x)=−
	(1−x)(1+x)2

	x		A		B		C
−		=		+		+
	(1−x)(1+x)2		1−x		1+x		(1+x)2

−x = A(1+2x+x²)+B(1−x²)+C(1−x) A+B+C=0 2A−C=−1 A−B=0 B=A 2A+C=0 2A−C=−1 B=A C=−2A 4A=−1

	x		1	1		1	1		1	1
−		=−			−			+
	(1−x)(1+x)2		4	1−x		4	1+x		2	(1+x)2

	1
∑n(−1)nxn−1=−
	(1+x)2

	1
∑n=1n(−1)nxn−1=−
	(1+x)2

	1
∑n=0(n+1)(−1)n+1xn=−
	(1+x)2

	1
∑(n+1)(−1)nxn=
	(1+x)2

	1		1		1
S(x)=−		(∑xn)−		(∑(−1)nxn)+		(∑(n+1)(−1)nxn)
	4		4		2

	1		1		1
Sn=−		−		(−1)n+		(n+1)(−1)n
	4		4		2

	1		1
Sn=−		+		(2n+1)(−1)n
	4		4