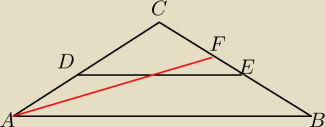
zadanie nr 13 6latek: Wykazac ze dowolny odcinek zawarty wewnatrz trojkata jest mniejszy od najdluzszsego boku tego trojkata Wydaje mi sie ze moze to byc odcinek czarny i takze czerwony

6latek:

PW: Zupełnie dowolny zawarty w trójkącie (nie musi mieć końców na brzegu trójkąta).

6latek: Jest to zadanie oznaczone jako trudne Ani tu nierownosc trojkata ,ani tw o lamanej .

Adamm: bez straty ogólności brzeg odcinka leży na brzegu trójkąta, bo możemy go zawsze przedłużyć wtedy odcinek d tworzy trójkąt który ma kąt α wspólny z jednym bokiem, powiedzmy a

c		b		d		a		b		c
	=		=		>		=		=
sinγ1		sinβ1		sinα		sinα		sinβ		sinγ

zatem β>β₁ oraz γ>γ₁, co przeczy temu że w dowolnym trójkącie kąty dodają się do 180^o

Adamm: zrobiłem dosyć dużą gafę, zignoruj

Bleee: Wystarczy zrobić okrąg o środku w A i promieniu AB i pokazać że trójkąt go nigdzie nie przecina.

Bleee: A skoro AC jest nie dłuższe niż promień okręgu to nie przecina tego okręgu więc odcinek BC nie ma części wspólnej z okregiem. Wiec każdy odcinek poprowadzona z wierzchołka A będzie krótszy od AB. Sytuacje kiedy odcinek nie startuje z wierzchołka A (lub B) można łatwo wykazać ze będą to odcinki krótsze od tych pociagnietych z tychże wierzchołków (tw. Talesa)

6latek: OK Blee