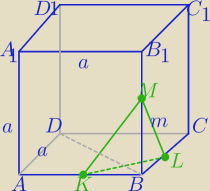
stereo anx: Punkty K, L, M są środkami krawędzi AB, BC, BB₁ sześcianu ABCDA₁B₁C₁D₁. a) Jaka część objętości sześcianu stanowi objętość ostrosłupa KLMB? b) Wiedząc dodatkowo, że odległość wierzchołka B od płaszczyzny KLM jest równa pierwiastek z 3, oblicz długość krawędzi sześcianu. Punkt a mam policzony (1/48 V), ale punkt B mi nie wychodzi. Czy ten odcinek padający na płaszczyznę KLM będzie padał dokładnie na wysokość trójkąta KLM?

anx: .

xxx: d=√3− odległość punktu B od pł. KLM ( wysokość ostrosłupa KLMB opusczona na ΔKLM}

	1		1		1		1		1		1
VKLMB=		*		*(		a*		a)*		a=		a3
	3		2		2		2		2		48

lub

	1
VKLMB=		*PΔKLM*d
	3

	a√2
ΔKLM − Δ równoboczny o boku m=
	2

1		1		(0.5√2a)2√3
	a3=		*		*√3
48		3		4

dokończ

anx: Dziękuję

Mila:

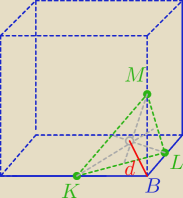
Julia: Czy ktoś chciałby mi pokazać która na tym rysunku to długość d ponieważ nie umiem tego zrozumieć

Mila: d− jedna z wysokości ostrosłupa KLMB−to jest odcinek poprowadzony z punktu B pod kątem prostym do płaszczyzny ΔKLM, który jest równoboczny. Spodek tej wysokości leży na przecięciu wysokości ΔKLM.

xyz:

Mila: dla xyz .