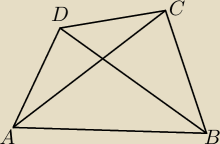
Zadanie nr 13 6latek: Wykazac z e suma przekatnych czworokata jest mniejsza od obwodu czworokata zas wieksza od polowy obwodu tego czworokata Z poprzedniego zadania mam ze

	AB+BC+CD+DA
AC<
	2

	AB+BC+CD+DA
BD<
	2

AC+BD<AB+BC+CD+DA teraz jak wyjasnic ze suma tych przekatnych jest wieksza od polowy obwodu tego czworokata Czy wysnuc wniosek z poprzednich obliczen?

Krzysiek60: Jeśli ktoś odpowie to dziekuke

wredulus_pospolitus: z nierówności trójkąta: |AC| < |AB| + |BC| |AC| < |AD| + |CD| |BD| < |AD| + |AB| |BD| < |BC| + |CD| więc: 2(|AC| + |BD|) < 2*(|AB| + |BC| + |CD| + |AD|) c.n.w.

Krzysiek60: Dziękuję bardzo

iteRacj@: To ja dodam jeszcze sposób na wykazanie, że suma przekątnych czworokąta jest większa od połowy jego obwodu. Ale wykonaj to Krzysiek sam. Przez S oznaczmy punkt przecięcia przekątnych. Skorzystaj z nierówności trójkąta kolejno dla ΔABS, ΔBCS, ΔCDS, ΔDAS. Po dodaniu stronami jest wynik.

iteRacj@: I trzeba pamiętać, że dzień zaczynający się od geometrii to zawsze jest dobry dzień.

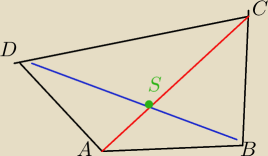
6latek: AS+SB>AB BS+SC>BC SC+DS>CD DS+AS>AD 2AS+2SC+2DS+2SB>AB+BC+CD+AD 2(AS+SC+SD+SB)>AB+BC+CD+AD

	AB+BC+CD+AD
AS+SC+SD+SB>
	2

AS+SC=AC SD+SB=DB

	AB+BC+CD+AD
AC+DB>
	2

c.j. t. w.