Wyznacz przedziały monotoniczności funkcji
x: Wyznacz przedziały monotoniczności funkcji f(x)= x2 −3x +3ln(x+1)
Mogę prosić o wytłumaczenie? Nie bardzo wiem z czym to się "je"... Czy należy zacząć od
policzenia pochodnej?
12 lut 23:22
wredulus_pospolitus:
należy zacząć od wyznaczenia dziedziny
później dopiero liczymy pochodną
13 lut 00:52
x: Mogę przyjąć, że dziedzina to zbiór liczb rzeczywistych, czy trzeba to jakoś inaczej wyliczyć?
Przykład pewnie jest łatwy, ale ja jestem całkowicie zielona w tym.
13 lut 09:52
Jerzy:
Jedyny warunek, to : x + 1 > 0 ⇔ x > −1 , czyli: D = (−1.+∞)
Teraz licz pochodną.
13 lut 09:58
13 lut 10:07
Jerzy:
Teraz trzeba ustalić znak pochodnej.
13 lut 10:09
x: Czyli pochodną przyrównuje do zera?
13 lut 10:12
Jerzy:
Nie musisz, bo nie ma w zadaniu mowy o ekstremach lokalnych.
Sprowadź to wyrażenie do wspólnego mianownika i ustalaj znak pamiętając,
że mianownik jest stale dodatni.
13 lut 10:14
x: | | 2x2 − x | | x(2x−1) | |
Po sprowadzaniu otrzymałam |
| czyli |
| |
| | x+1 | | x+1 | |
| | 1 | |
I miejsca zerowe to x=0 oraz x= |
| |
| | 2 | |
I teraz rysuję.
Czy o to chodziło?
13 lut 10:23
Jerzy:
Tak,teraz naszkicuj sobie wykres samego licznika, bo jego znak decyduje o znaku pochodnej
i ustal jak się zmienia ten znak.
13 lut 10:24
x:
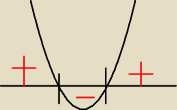
Dobrze, a skąd wynika to, że mianownik jest stale dodatni?
13 lut 10:34
Jerzy:
A jaka jest dziedzina tej funkcji ?
13 lut 10:35
x: Dziedzina = (−1.+∞)
13 lut 10:41
Jerzy:
A jaki ma znak mianownik w tym przedziale ?
13 lut 10:45
x: Dodatni
13 lut 10:49
Jerzy:
Ano właśnie, czyli mianownik pochodnej jest stale dodatni.
13 lut 10:51
x: Już rozumiem, dziękuję za cierpliwość.
Czyli rysunek jaki wykonałam to przedziały monotoniczności tej funkcji? I odczytuję, że funkcja
| | 1 | | 1 | |
jest malejąca dla x∊ (−∞, |
| ) i rosnąca dla x∊ ( |
| ,∞)? |
| | 2 | | 2 | |
13 lut 11:06
Jerzy:
NIE ! Rysunek ,który sporzadzilaś, to wykres licznika pochodnej.
Na jego podstawie ustalasz w jakich przedzialach pochodna jest dodatnia ( tam funkcja jest
rosnąca ) , a w jakich jest ujemna ( tam funkcja jest nalejąca ) W miejscach zmiany znaku
pochodnej funkcja ma ekstrema lokalne.
Pamietaj o dziedzinie funkcji, bo ona tylko tam istnieje.
13 lut 11:10
Pau: To pierwsza funkcja jaką badam i dalej nie bardzo wiem jak to potraktować...
13 lut 20:18
x: Edit − zły nick wbiłam.
13 lut 20:19
Jerzy:
Funkcja rośnie w przedziale (−1,0) , maleje w przedziale (0,1/2) i rośnie w przedziale (1/2,∞)
13 lut 21:02