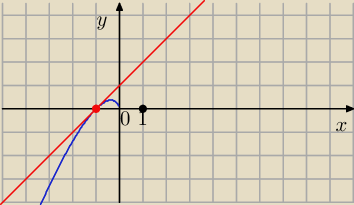
Równanie prostej stycznej do wykresu funkcji 123: Nie wiem czy dobrze zrobiłem Równanie prostej stycznej do wykresu funkcji f(x) = x ln( −x) w punkcie ( −1 , F(−1)) F(−1) = −1ln1 = ln 1⁻1 = ln1 = 0 P=(−1.0)

	1		1
F'x = (x)' * (ln(−x))' = 1 *		= −
	−x		x

F'(x₀) = F'(−1) = 1 y−0=1(x+1) y=x+1

Janek191:

	−1
f '(x) = ln( − x) + x* ( − 1*		) = ln ( −x) + 1
	x

123: nie rozumiem xD

Janek191: Pochodna była źle obliczona: ( f * g) ' = f ' * g + f * g'

123: a dzięki

Janek191: