. sylwiaczek: Prosta x−y−5=0 zawiera bok AB trojkata ABC, prosta 2x+y−13=0 zawiera bok BC natomiast prosta 3x−y−7=0 zawiera dwusieczna kata BAC znajdz wierzcholki tego trojkata. obliczyłam A(1,−4) B(6,1) tgα=1/2 to jest kat miedzy prosta dwusiecznej a prosta AB to juz praktycznie koncowka zadania bo zostalo obliczyc C ale nie wiem jak

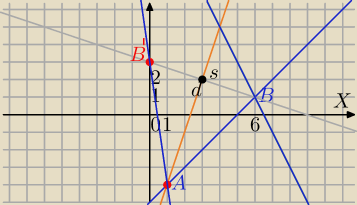
Mila: AB: x−y−5=0⇔y=x−5 BC: 2x+y−13=0⇔y=−2x+13 prosta 3x−y−7=0 − dwusieczna kąta BAC ⇔y=3x−7 1) A=(1,−4), B=(6,1) 2) Szukam punktu B' symetrycznego do B względem prostej d m⊥d

	1
m: y=−		x+b i B∊m⇔b=3
	3

	1
m: y=−		x+3
	3

Punkt przecięcia d i m

	1
−		x+3=3x−7
	3

x=3, y=2 S=(3,2) − środek BB'

	x+6		y+1
3=		i 2=		⇔
	2		2

x=0 i y=3 B'=(0,3) 3) Równanie prostej AB' y=ax+3 i −4=a+3 y=−7x+3 4) Punkt C −7x+3=−2x+13 −5x=10 x=−2 y=17 C=(−2,17) 5) A=(1,−4), B=(6,1),C=(−2,17)

sylwiaczek: skad wiadomo ze B' lezy na prostej AC?

czarna inez: Punkt S jest punktem przeciecia sie dwusiecznych natomiast srodek okregu wpisanego w trojkat wlasnie lezy w tym punkcie i dlatego odleglosc SB jest promieniem okregu wpisanego w ten trojkat Stad wniosek punkt B' lezy na prostej wyznaczajacej bok AC

Mila: Punkt S należy do dwusiecznej kąta A, ∡BAS≡∡B'AS

sylwiaczek: ale czy B' nie powinno byc pod katem prostym do dwusiecznej wzgledem ktorej był odity?

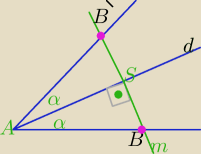
Mila: Prosta SB jest prostopadła do dwusiecznej, masz tam napisane, że m⊥d BS⊥AS, |BS|=|SB', bo S jest środkiem odcinka BB' ΔABB'− Δrównoramienny