Zadanie nr 9
czarna inez: Znalezc punkt polozony wewnatrz wypuklego czworokata taki aby suma jego odleglosci od
wierzcholkow danego czworokata byla mozliwie najmniejsza
W odpowiedzi mam tylko .Punkt przeciecia przekatnych
12 lut 16:33
ite:
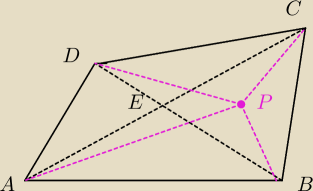
Zauważ, że |DE|+|EB|<|DP|+|PB| dla każdego P∉ BD. Dlaczego? Skorzystaj z nierówności trójkąta.
To samo dla drugiej przekątnej.
12 lut 16:47
czarna inez: Juz chyba rozumiem
Odpisze za chwile . dzieki
12 lut 16:57
czarna inez: DE+EB=BD
BD≤DP+PB
AE+EC=AC
AC≤AP+PC
Wiec zeby suma odleglosci punktu P od wierzcholkow byla najmniejsza musi byc
DP+PB=BD i
AP+PC=AC
A to oznacza ze punkt P musi lezec na przecieciu sie przekatnych czworokata
12 lut 17:31
czarna inez: Czy dobrze ?
czy nalezy to inaczej uzasadnic?
12 lut 17:41
czarna inez:
12 lut 18:36
iteRacj@:
1/ dla każdego P∉ BD: |DP|+|PB|>|BD| → odcinek BD jest zbiorem punktów, dla których suma
odległości od wierzchołków B i D jest możliwie najmniejsza,
2/ dla każdego P∉ AC: |AP|+|PC|>|AC| → odcinek AC jest zbiorem punktów, takich że suma ich
odległości od wierzchołków A i C jest możliwie najmniejsza,
3/ punktem, dla którego suma odległości od wierzchołków A, B, C i D jest możliwie najmniejsza,
będzie punkt należący do obu odcinków czyli ich punkt wspólny E.
12 lut 20:44
12 lut 20:52
 Zauważ, że |DE|+|EB|<|DP|+|PB| dla każdego P∉ BD. Dlaczego? Skorzystaj z nierówności trójkąta.
To samo dla drugiej przekątnej.
Zauważ, że |DE|+|EB|<|DP|+|PB| dla każdego P∉ BD. Dlaczego? Skorzystaj z nierówności trójkąta.
To samo dla drugiej przekątnej.