Zadanie nr 7 czarna inez: W wypuklym 13 −kacie poprowadzono wszystkie przkatne ktore podzielily dany wielokat na szereg rozlacznych wielokatow takich ze zaden z punktow tych przekatnych nie jest punktem wewnetrzym zadnego z otrzymanych wielokatow Ile co najwyzej bokow moze miec wielokat w zbiorze otrzymanych wielokatow Nie wiem o co tutaj chodzi .

czarna inez: Podbijam

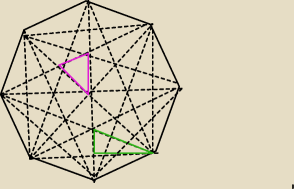
iteRacj@: Różowy trójkąt spełnia warunki zadania, zielony nie. Czy to jest właściwa interpretacja treści?

czarna inez: W odpowiedzi jest 13−kat foremny

iteRacj@: Ja nie rozwiązuję tego zadania. Po prostu się zastanawiam nad treścią i pytam mądrzejszych, czy to zagadnienie dobrze zrozumiałam.

czarna inez: OK

czarna inez: Jest w innym zbiorze tak Bokami kazdego wielokata moga byc co najwyzej dwie przekatne wychodzace z danego wierzcholka , a wiec liczba bokow kazdego wielokata nie moze byc wieksza od 13 . Wystarczy zatem podac przyklad takiego 13−kąta . W tym celu wezmy pod uwage 13−kąt foremny i poprowadzmy z kazdego wierzcholka dwie najdluzsze przekatne . Otrzymamy w ten sposob 13−kat foremny przy czym srodek okregu opisanego na tym 13− kacie pokrywa sie ze srodkiem okregu opsanego na 13− kacie danym . Dlaczego tak ?

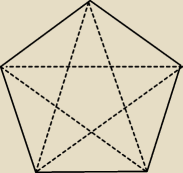
iteRacj@: Najłatwiej 13−kąt na rysować w geogebrze https://www.geogebra.org/geometry/ywasympm Przy nieparzystej ilości wierzchołków z każdego wierzchołka wychodzą dwie najdluższe przekątne i wygląda to inaczej niż w 8−kącie z 20:03. Pięciokąt foremny narysowałam pomocniczo, ale zostawiam ten rysunek, może się przyda komuś, kto będzie chciał odpowiedzieć na pytanie.