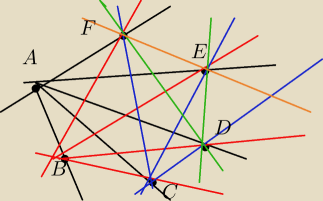
Zadanie nr 4 czarna inez: Na plaszczyznie danych jest 6 punktow Przez kazde dwa z nich prowadzimy prosta Ile co najwyzej prostych mozna w ten sposob otrzymac Na rysunku mam ze tych prostych jest 15 jednak musi byc na to jakis wzor do obliczenia gdyz jesli tych punktow byloby np 20 to trudno byloby policzyc

Tadeusz:

6*5
2

albo 5+4+3+2+1

czarna inez: czyli mozna zapisac ze ilosc tych prostych to

	n(n−1)
p=
	2

wredulus_pospolitus: zacznijmy od tego −−− czy te punkty masz podane na rysunku ? Jeżeli nie to można je wszystkie ustawić na jednej prostej i wynikiem będzie 1 w przeciwnym razie można np. skorzystać z kombinatoryki.

czarna inez: tak jak na rysunku jak skorzystac z kombinatoryki ?

czarna inez:

wredulus_pospolitus: skoro wiemy, że żadne trzy punkty nie są współliniowe (czyli prosta może przechodzić przez co najwyżej dwa punkty) to: 1) Liczymy ile istnieje takich prostych, że zawierają dokładnie 2 punkty z tych sześciu. 2) Wybieramy pierwszy z tych punktów, na '6 sposobów'. 3) Wybieramy drugi z tych punktów, na '5 sposobów'. 4) Dzielimy to przez '2' ponieważ wybór A i B oraz B i A daje tą samą prostą, więc nie możemy tego liczyć podwójnie

	6*5
5) I otrzymujemy to co Tadeusz napisał:
	2

wredulus_pospolitus:

	n(n−1)
Ogólnie będzie to
	2

czarna inez: Dziekuje Ci