Zadanie Kamil: Cześć, mam takie zadanie do zrobienia W jaki sposób wyznaczamy ekstrema lokalne funkcji y= f(x) przy wykorzystywaniu pochodnej ? (Uwaga: napisz jakie własności pochodnej należy sprawdzić i na jakiej podstawie wyciągamy funkcji) Wcale tego nie rozumiem Zrobiłem tyle: 1.Wyznaczamy dziedzinę funkcji y=f(x) 2.Liczymy pochodną funkcji y= f'(x) 3.Wyznaczamy dziedzinę pochodnej 4. Przyrównujemy pochodną do zera i ją obliczamy f'(x)=0 i dalej nie wiem co robić i czy to jest dobrze ? Czy ktoś pomoże ?

Adamm: wszystkie punkty które nie są wewnętrzne, wszystkie punkty w których pochodna nie istnieje, oraz te w których się zeruje je wszystkie trzeba sprawdzić

Adamm: np. y = |x| nie ma pochodnej w x = 0, ale ma tam ekstremum y = x, x≥0, ma pochodną jednostronną w x = 0, różną od 0, ale mimo to ma tam ekstremum y = x³ ma pochodną w zerze, ale nie ma tam ekstremum

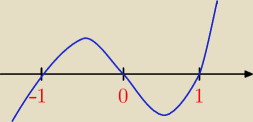
xyz: po prostu jak zrobisz f'(x) = 0 to rysujesz wykres pochodnej i badasz czy pochodna zmienila znak przyklad: f(x) = x⁴ − 2x² + 1 D_f = ℛ f'(x) = 4x³ − 4x D_f' = ℛ f'(x) = 0 4x³ − 4x = 0 4x(x²−1) = 0 x = 0 lub x² − 1 = 0 x = 0 lub (x−1)(x+1) = 0 x = 0 lub x=1 lub x=−1 Rysuje wezyk od prawej i teraz od gory (bo mam 4 > 0 przy najwyzszej potedze iksa) i kazde miejsce zerowe jest jednokrotne wiec po prostu przechodzi przez te miejsca w punkcie x = − 1 mamy minimum lokalne (bo wykres pochodnej zaczyna sie ponizej zera a potem przechodzi nad) w punkcie x = 0 mamy maksimum lokalne(bo przechodzi z ponad osi do ponizej osi) i w koncu x = 1 mamy minimum lokalne(bo idzie z dolu do gory)