ile wynoszą miary kątów
ika: Promień okręgu opisanego na trójkącie prostokątnym ma długość r. Wysokość opuszczona
zwierzchołka kąta prostego jest cztery razy krótsza od przeciwprostokątnej. Miary
kątów ostrych tego trójkąta wynoszą
10 lut 22:13
Mila:
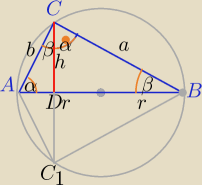
|AB|=2r
β<α
W ΔC
C1B:
2h=2r*sin(2β)
2β=30
o
β=U{15
o}
α=90
o−15
o
α=75
o
=========
10 lut 22:31
ika: Czy można zadanie rozwiązać inną metodą?
11 lut 11:13
Eta:
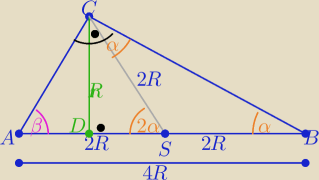
| | R | | 1 | |
ΔDSC "ekierkowy" sin2α= |
| = |
| to 2α=30o |
| | 2R | | 2 | |
zatem
α=15
o to
β=75
o
======================
i to wszystko

11 lut 12:53
PW: Rozwiążę bardziej skomplikowanie (a kto mi zabroni?), za to bez korzystania z "r".
Niech wysokość opuszczona na przeciwprostokątną dzieli ją na odcinki x, y.
Z treści zadania
4h = x + y,
a więc
(1) 16h
2 = (x+y)
2.
Jednocześnie z twierdzenia Pitagorasa
(2) (x+y)
2=a
2+b
2
i po podstawieniu (2) w (1)
16h
2 = a
2+b
2
| | 1 | | 1 | |
16 = |
| + |
| |
| | sin2α | | sin2(90°−a) | |
| | cos2α+sin2α | |
16 = |
| |
| | sin2αcos2α | |
| | 1 | |
sin(2α) = |
| (bo sinα>0) |
| | 2 | |
Jeżeli α jest mniejszy od β, czyli α < 45°, to
2α = 30°
α = 15°,
β = 75°.
11 lut 14:21
Eta:
Jak ktoś "lubi" dużo pisać , to...........

11 lut 19:34
ika: Dziękuję za odpowiedź. Rzeczywiście trochę skomplikowane metody rozwiązania tym bardziej dla
mnie gdyż funkcji trygonometrycznych jeszcze nie omawialismy.. A może jest jeszcze inna metoda
rozwiązania?
11 lut 20:49
Eta:
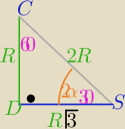
Tak , jak napisałam trójkąt DSC "ekierkowy" 30
o,60
o,90
o ( bez trygonometrii)
to
2α=30
o ⇒
α=15
o
11 lut 21:29
Mila:
ika , w której jesteś klasie?
11 lut 22:38
ika: Chodzę do kl 7 SP
11 lut 23:32
ika: Rozwažam to zadanie i dalej nie rozumiem rozwiązania−Kąt ekierkowy − kąt 30 st leży naprzeciw
krótszej przyprostokatnej więc kąt DSC wydaje się mieć 60 stopni (Trójkąt ASC wydaje się
równoboczny) a kąt SCD wówczas ma 30 stopni W rozwiązaniu jest jednak odwrotnie. Proszę o
wskazówki
12 lut 11:33
Jerzy:
A o którym rysunku teraz mówisz ?
12 lut 11:38
Mila:
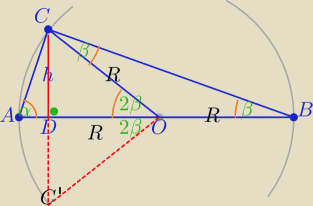
|∡ACB|=90
o
α+β=90
o
|AB|=2R
| | 1 | | R | |
h= |
| *2R= |
| z treści zadania |
| | 4 | | 2 | |
1) Rysuję trójkąt symetryczny do trójkąta CDO względem prostej AB⇔
ΔCDO≡C'DO
2)ΔCC'O jest trójkątem równobocznym o bokach:
CC'=2h=R, |CO|=R, C'O|=R⇔Δ ma kąty równe po 60
o.
3) 4β=60
β=15
o
α=90
o−15
0=75
=============
12 lut 16:46
ika: Uprzejmie dziękuję, już rozumiem

12 lut 20:06
Mila:
Następnym razem przypominaj na jakim poziomie edukacji ma być rozwiązanie.

12 lut 20:33
ika: Oczywiście

12 lut 20:38
 |AB|=2r
|AB|=2r



 Tak , jak napisałam trójkąt DSC "ekierkowy" 30o,60o,90o ( bez trygonometrii)
to 2α=30o ⇒ α=15o
Tak , jak napisałam trójkąt DSC "ekierkowy" 30o,60o,90o ( bez trygonometrii)
to 2α=30o ⇒ α=15o
 |∡ACB|=90o
α+β=90o
|AB|=2R
|∡ACB|=90o
α+β=90o
|AB|=2R


