geometria analityczna Wąsko!: Punkty A (−1,−2) i B (2,0) są kolejnymi wierzchołkami kwadratu ABCD. Wyznacz współrzędne wierzchołków C i D. Pomoże ktoś?

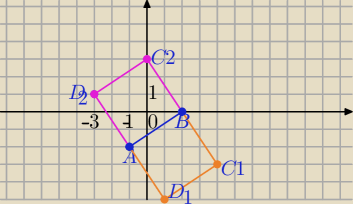
xxx: 1) AB^→=[3,2] 2) BC⊥AB BC^→=[2,−3] lub [−2,3] B=(2,0)→T_[2,−3]⇒C₁=(4,−3) lub C₂=(0,3) 3) AD || BC A=(−1,−2)→T_[2,−3]⇒D₁=(1,−5) lub D₂=(−3,1)

Barbara_123: Koledze chyba chodziło o rozwiązanie OBLICZENIEM...

Mila: No cóż, niech kolega sam się wypowie.

Wąsko!: Pani Barbara₁23 ma racje

Wąsko!: Bardzo proszę o pomoc, jutro mam kartkówkę z tego typu zadań!

Mila: Zaraz

Mila: W której klasie jesteś ?

Eta: W maturalnej

Wąsko!: Ja w 2 technikum ekonomicznego z rozszerzoną matematyką

Mila: Wzór na odległość punktu od prostej miałeś?

Wąsko!: Próbowałem to rozwiązać na wiele sposobów, ale nic nie wychodzi...wektory, odległość między punktami...

Wąsko!: nie, tego wzoru nie

Wąsko!: chwila, sprawdzam, jednak mam d= wartość bezwględna z Ax0+By0+C podzielone przez sumę pierwiastka kwadratów A+B

Wąsko!: Nadal nie mam pomysłu na rozwiązanie

Wąsko!: Nie rozumiem tego

Eta: Rozwiązanie w poście z 17.27 podane przez .... za pomocą wektorów ! To najłatwiejszy sposób!

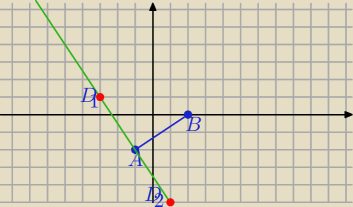
Mila: A (−1,−2) i B (2,0) 1) |AB|=√3²+2²=√13 − długość boku kwadratu 2) prosta AB: y=ax+b A (−1,−2) i B (2,0) −2=−a+b 0=2a+b ====== odejmujemy stronami:

	2		2
−2=−3a, a=		, −2=−		+b
	3		3

	2		4
a=		, b=−
	3		3

	2		4
AB: y=		x−
	3		3

3) AD⊥AB prosta AD:

	3		3
y=−		x+b i A∊prostej ⇔−2=−		*(−1)+b, b=−312
	2		2

	3		7
y=−		x−
	2		2

4) |AD|=√13 D=(a,b) i leży na prostej AD⇔

	3		7
D=(a,−		a−		)
	2		2

|AD|²=√13²=(a+1)²+(−1.5a−3.5+2)² a²+2a+1+(−1.5a−1.5)²=13 a²+2a+1+2,25a²+4,5a+2,25=13 3.25a²+6.5a−9.75=0 /*4 13a²+26a−39=0 /:13 a²+2a−3=0 a=−3 lub a=1

	9		7
D1=(−3,		−		0=(−3,1) lub D2=(1, −5)
	2		2

Licz może sam punkt C Za chwilę dokończę

Eta: Tylko wektorami ! .... bo szkoda czasu

Wąsko!: Dziękuję ! <3333

Mila: Współrzędne punktu C AC⊥AB

	3
y=−		x+b i B= (2,0) ∊prostej
	2

	3
0=−		*2+b, b=3
	2

y=−1.5x+3 C=(a,−1.5a+3) |AC|²=13=(a−2)²+(−1.5a+3−0)² a²−4a+4+2,25a²−9a+9=13 3.25a²−13a=0 a*(3.25a−13)=0

	13
a=0 lub a=		=4
	3,25

C₌(0,3) lub C₂=(4,−1.5*4+3)=(4,−3) ====================== To najdłuższy sposób. Naucz się wektorów.