Znajdź równanie prostej będącej rzutem prostej l : 𝑥−34=𝑦+65=𝑧−2 na płaszczyz zzzzzzzzzzz: Znajdź równanie prostej będącej rzutem prostej l : ^𝑥−3₄=^𝑦+6₅=^𝑧₋₂ na płaszczyznę 2𝑥+𝑦−3𝑧+8=0 .Jak to rozwiązać ? jestem w stanie bez problemu wuznaczyć wektor kierunkowy prostej który jest wektorem normalnym płaszczyzny natomiast nie wiem co dalejmoże źle rozumiem zadanie ale np oitrafie wyznaczyć punkt na prostej i go wstawić w równanie szukanej prostej.Nie wiem pomocy!

ABC: weź dwa punkty z tej wyjściowej prostej i zrzutuj oba na płaszczyznę , a potem napisz równanie przechodzącej przez te dwa rzuty

zzzzzzzzzzz: aha o ot chodziło , dobrze dzięki źle zrozumiałem treść zadania

zzzzzzzzzzz: Nie umiem zrzutować tych punktów potrafie je wyznaczyć ale nie potrafie zrzutować jak to zrobić

ABC: tak się chwaliłeś że wektor normalny płaszczyzny umiesz, a rzutować nie umiesz? prowadzisz prostopadła do płaszczyzny przechodzącą przez ten punkt i patrzysz gdzie przebija ona płaszczyznę

zzzzzzzzzzz: mam punkty a jakie jest równanie prostej przechodzącej przez dwa rzuty ?

ABC: Wektor skonstruuj przy użyciu tych dwóch rzutów

zzzzzzzzzzz: oks

zzzzzzzzzzz: i co dalej ?

zzzzzzzzzzz: w sumie to jest wektor kierunkowy szukanej prostej

zzzzzzzzzzz: to pewnie miejscami zerowymi będzie jeden punkt który jest rzutem tak ?

ABC: za mało amfy bierzesz... masz punkt i wektor to masz równanie kierunkowe prostej

zzzzzzzzzzz: no czyli ten skonstruowany wektor z rzutów to jest a,b,c w wzorze ^x−x0_a=^y−y0_b=^z−z0_c? a tym X0 y0 z0 to punkt który jest rzutem ?

xxx: π: 2𝑥+𝑦−3𝑧+8=0 l: x=3+4t y=−6+5t z=0+2t, t∊R A=(3,−6,0)∊l t=1, B=(7,−1,2)∊l 2) Prosta prostopadła do π, A∊prostej k^→=[2,1,−3] k: x=3+2s y=−6+s z=−3s, s∊R 3) Punkt przebicia płaszczyzny ( rzut p. A na płaszczyznę) 2*(3+2t)−6+t−3*(−3t)+8=0

	4
t=−
	7

	13		46		12
A'=(		,−		,		)
	7		7		7

4) Rzut punktu B na płaszczyznę prosta m⊥π, B∊m m: x=7+2u y=−1+u z=2−3u , u∊R

	15
u=−
	14

	34		29		73
B'=(		,−		,		)
	7		7		14

5) Prosta A'B'

	17		49
A'B'→=[3,		,		]
	7		14

posprawdzaj obliczenia i dokończ

Jerzy: Zadanie na dwie linijki,a tak go komplikujecie.

xxx: Rozwiąż Jerzy.

Eta:

jc: Przecięcie prostej x=3+4t, y=−6+5t, z= 2t z płaszczyzną 2x+y−3z+8=0: 2(3+4t)+(−6+5t)−3*2t+8=0 7t+8=0, no i wychodzi jakiś ułamkowy wynik. t=−8/7, podstawiasz i masz przecięcie. u=(4,5,2) kierunek prostej, v=(2,1,−3) wektor prostopadły do płaszczyzny.

	v*u		1
w=u −		v =		(1,8,7) kierunek szukanej prostej.
	v2		2

Masz wszystko i piszesz wzór prostej.

jc: Jakaś usterka w rachunkach.

	8+5−6		1		1
w=(4,5,2) −		(2,1,−3)=(4,5,2)−		(2,1,−3) =		(6,9,7)
	4+1+9		2		2

Teraz jest dobrze.

Satan: @jc, dlaczego wektor kierunkowy szukanej prostej jest takiej postaci?

jc: Dokończenie. x=3−32/7=(21−32)/7=−11/7 y=−6−40/7=−82/7 z=−16/7 Prosta: x=−11/7+6t, y=−82/7+9t, z=−16/7 +7t

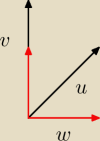
jc: Od u odejmujesz rzut u na kierunek v. Zostaje w.

Jerzy: Do danej płaszczyzny prowadzisz płaszczynę prostopadłą zawierającą daną prostą. Równanie krawędziowe tych dwóch płaszczyzn wyznacza równanie rzutu.

jc: Inaczej. w=u−kv, k dobierasz tak, aby w był prostopadły do v. 0=w*v=u*v − k v*v k= u*v/ v²

Jerzy: Wektor normalny tej nowej płaszczyzny, to iloczyn wektorowy wektora kierunkowego danej prostej i wektora normalnego podanej płaszczyzny.

jc: Jerzy, aby poprowadzić płaszczyznę prostopadłą musisz znaleźć wektor prostopadły do wektora u i v. Możesz to zrobić licząc iloczyn wektorowy. Jeśli chcesz mieć prostą w postaci parametrycznej musisz rozwiązać układ równań lub policzyć kolejny iloczyn wektorowy. Łatwiej policzyć dwa iloczyny skalarne (policz liczbę działań arytmetycznych).

jc: Dwa iloczyny skalarne: 6 mnożeń + 4 dodawania dwa iloczyny wektorowe: 2 (6 mnożeń + 3 odejmowania) = 12 mnożeń + 6 odejmowań. No dobrze, nie jest tak źle. Dodatkowo u mnie jest 6 mnożeń i 3 odejmowania. Przegrywam jednym działaniem. Jednak rzutowanie bardziej mi się podoba.

Jerzy: @jc ..... chyba wymieniliśmy uwagi wczoraj przy podobnym zadaniu.Niech student wybiera sposób.

jc: We wczorajszym zadaniu była duża różnica w złożoności rozwiązania. Tu jest niewielka. Ale faktycznie, prawie każde zadanie z geometrii analitycznej można rozwiązać na kilka sposobów.