znajdź liczbę
Mata: Jeśli liczbę dwucyfrową podzielimy przez sumę jej cyfr, to otrzymamy 5 i resztę 11.Jeśli zaś w
tej liczbie przestawimy cyfry i otrzymaną liczbę podzielimy przez sumę jej cyfr, to otrzymamy
5 i resztę 2. Jaka to liczba?
Proszę o pomoc w rozwiązaniu tego zadania inną łatwiejszą metodą niż układ równań z dwiema
niewiadomymi.
10 lut 11:54
Jerzy:
Skoro masz dwie niewiadome,to musisz mieć dwa niezależne równania.
10 lut 11:56
Mata: Mój nauczyciel matematyki lubi jak zadania są rozwiązane kilkoma sposobami, w dodatku metodą
zrozumiałą dla uczniów nawet z niższych klas podstawówki.
10 lut 12:01
Jerzy:
Ale nawet twój nauczyciel głową muru nie przebije.
10 lut 12:03
wredulus_pospolitus:
1) zauważamy, że a+b > 11
2)
| 10a + b | | a+b | | 9a | | 4a + 4b + 5a − 4b | |
| = |
| + |
| = 1 + |
| = |
| a+b | | a+b | | a+b | | a+b | |
| | 5a − 4b | | 11 | |
= 5 + |
| = 5 + |
| |
| | a+b | | a+b | |
3) więc
5a − 4b = 11
4)
podstawiamy kolejne liczby:
a = 1 odpada (bo b<0)
a = 2 odpada (bo b<0)
a = 3 pasuje b=1 , ale a+b < 11
a = 4 odpada (bo b∉Z)
a = 5 odpada (bo b∉Z)
a = 6 odpada (bo b∉Z)
a = 7 pasuje b = 6 oraz wtedy a+b = 13 > 11
a = 8 odpada (bo b∉Z)
a = 9 odpada (bo b∉Z)
Odp. Szukana liczba to 76.
Powiedzmy, że jest to 'inne, łatwiejsze' rozwiązanie
10 lut 12:19
Jerzy:
Z pewnością nauczyciel polubi to rozwiązanie,bo metoda jest zrozumiała nawet dla uczniów
niższych klas podstawówki
10 lut 12:24
Mata: Dziękuję za pomoc!
10 lut 12:25
wredulus_pospolitus:
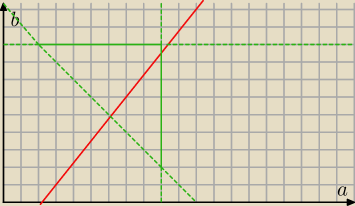
zamiast rozpisywać w (4) można byłoby także zrobić 'bardziej skomplikowaną rzecz i zrobić to
graficznie:
Interesuje nas jedynie obszar wewnątrz tych trzech zielonych prostych:
a = 9 (maksymalna cyfra)
b = 9 (maksymalna cyfra)
a+b = 11 (suma tych cyfr musi być większa od 11)
| | 5 | | 11 | |
interesuje nas prosta: b = |
| a − |
| |
| | 4 | | 4 | |
Już na wstępie widać, że tylko a = 7 , a = 8 i a = 9 nie leży poza rozpatrywanym obszarem.
Jedynie dla a = 7, b będzie całkowita.
10 lut 13:03