ekstremum Ada: Mam taka funkcję

x2−3
x−2

wyznaczajac jej dziedzine wypada 2 jakie jest ekstremum tej funkcji?

Jerzy: Najpierw policz pochodną.

PW: Bez pochodnej (warto próbować, czy nie można rozwiazać problemu metodami elementarnymi):

	x2−3		x2−4+1		(x−2)(x+2)+1		1		1
f(x)=		=		=		= (x+2)+		= (x−2)+		+4
	x−2		x−2		x−2		x−2		x−2

	1
Dla x>2 można skorzystać z nierówności a+		≥2 prawdziwej dla a>0 i mamy
	a

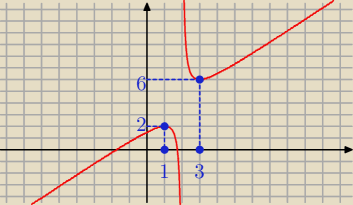
f(x) ≥ 2+4=6 dla x>2, przy czym równość ma miejsce dla x−2=1, tzn. dla x=3. Na przedziale (2,∞) funkcja osiąga minimum równe 6 (w punkcie x₀ = 3). A jak będzie na przedziale (−∞, 2)?

PW: