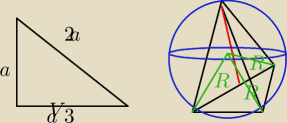
Stereometria gsasf: Podstawą ostrosłupa jest trójkąt prostokątny o kącie ostrym 30 stopni.Każda krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem 60 stopni. Oblicz stosunek objetosci ostroslupa do objetosci opisanej na nim kuli. Skoro w podstawie jest trójkąt prostokątny i sciany boczne są nachylone do płaszczyzny podstawy pod jednym kątem,to wysokość ostrosłupa będzie opadać na środku przeciwprostokątnej która jest równa 2a.

	H
Krawędź boczna jest nachylona do płaszczyzny podstawy pod katem 60 stopni więc		=tg60
	a

H=a√3

	a3
Vostr.=
	2

W sumie nawet nie wiem czy to co napisałem wyżej jest poprawne a dalej tym bardziej nie mogę wykombinować,bo ostrosłup nie jest prawidłowy.

gsasf: krawedzie boczne *

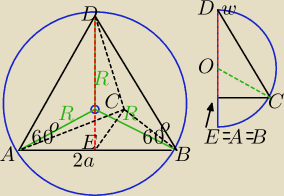iteRacj@: Wszystkie krawędzie boczne ostrosłupa są nachylone do płaszczyzny podstawy pod tym samym kątem. |<DAB|=|<DBA|=|<DCE|=60^o → ΔDAB równoboczny Wysokość ostrosłupa jest opuszczona na środek przeciwprostokątnej Δ w podstawie ostrosłupa. → D,A,B i środek kuli O leżą w jednej płaszczyźnie, należą do koła wielkiego i stąd da się wyliczyć promień kuli w zależności od a

gsasf: dzieki